特别感谢 Justin Drake，Dankrad Feist，Alex Obadia，Hasu，Anders Elowsson 和各位 hackmd 匿名者对这篇文章各个版本的审校和反馈。

当前，以太坊区块需要 64 到 95 个 slot（约15分钟）才能实现最终确定性。这是合理的，是在去中心化/最终确定性时间/开销曲线上的一个折衷取值：15分钟不算太长，而且与现有交易所的确认时间相当，它让用户能够在常规计算机上运行节点，即使因为存款大小为 32 ETH (而不是前期要求质押的 1500 ETH) 而出现了大量的验证者。

然而，我们仍然有充分的理由把最终确定性时间缩短为一个 slot。这是一篇研究现状综述，回顾了实现该目标的路线图。

当前以太坊 staking 的运作方式及依据

以太坊的 LMD GHOST + Casper FFG 共识是权益证明区块链中流行的两类主流共识算法间的折衷：

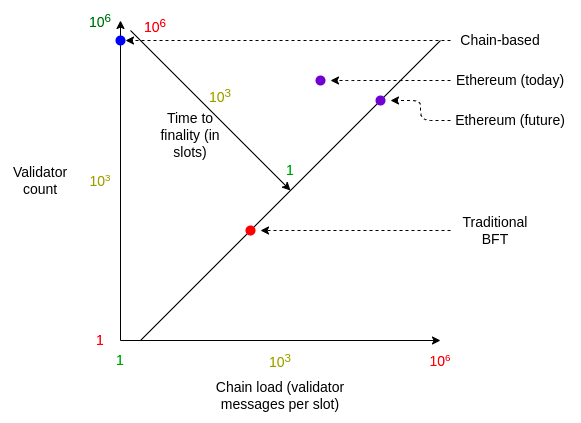
• 基于链的共识算法：每个 slot（一个预设的时间间隔，如以太坊中的 12 秒）生成一条消息（区块）。基于链的共识算法最大限度地提高了参与者的数量以及减少了链的负载，但很容易出现分叉，而且没有任何最终确定性的概念。
• 传统的 BFT (拜占庭容错) 共识算法：每个 slot 内，除了某个验证者生成一个区块外，每个验证者会生成两条消息（“attestation”，译者注：也就是“见证”），而且一个 slot 的区块在下一个 slot 开始之前实现了不可逆转的“最终确定性”。传统的 BFT 共识算法最大限度地缩短了实现最终确定性的时间，但是以链的高负载和仅支持少量的参与者为代价。

与单纯的基于链的系统不同，以太坊共识算法在每个 slot 都会并行对链头进行数以千计的见证投票。每一个 epoch（32 个 slot，或 6.4 分钟），所有活跃的验证者都有机会见证（attest）一次。两个 epoch 后，Casper FFG 最终确定性工具敲定（finalize）了区块，自此之后，回滚该区块需要至少三分之一的验证者销毁其质押存款：攻击成本会超过 400 万 ETH。这就区别于单纯的传统 BFT 系统，后者在一个 slot 后实现最终敲定。

因此，今天的以太坊实现的是：

• 适中的最终确定时间——与传统 BFT 在单个 slot 完成最终确定相比时间更长，但不是几周或几个月，或像基于链的共识算法那样未曾提供过
• 适中的链负载——每个 slot 会有数千条消息，但少于使用传统 BFT 时的数十万条信息
• 适中的节点数——成为一个验证者要求质押 32 ETH：与基于链的共识算法相比门槛更高，在基于链的共识算法中即使拥有很少量的 Token 也可以参与共识，但与传统 BFT 共识算法要求的超大量 Token 相比门槛低很多

以太坊对更高强度链负载的支持是由 BLS 签名聚合的效率提升来实现的。由于这些效率的提升，能实现高强度的链负载 (每秒消息量的角度) 得以转化为只需适中数据和 CPU 开销的链负载。

BLS 签名聚合的工作原理是将多个签名聚合成一个，这样，验证聚合后的签名只需每个参与者进行一次额外的椭圆曲线加法（不是乘法），并且 64 字节可以容纳任意数量参与者的签名，而每个参与者只需一个额外的位来存储。

基于链的共识算法和传统 BFT 共识算法的结合折衷，再加上源于 BLS 的纯效率提升，形成以太坊当前的共识算法。

那为何要改变它呢？

在使用上述推理开发出原初的以太坊共识协议后的几年内，我们得到了一个重大的好消息和一个重大的坏消息。

坏消息：混合型共识机制实际上有许多不可避免的问题

混合型共识机制结合了分叉选择规则以及最终确定性工具，前者用于逐个 slot 推进共识，后者用于后续敲定区块。混合型共识机制最大的问题是：

用户体验：大多数用户不愿为交易最终确定而等待 15 分钟。当前，即使交易所也通常认为资金存入在 12 到 20 次确认（约 3 到 5 分钟）后才“最终敲定”，尽管 12 到 20 次 PoW 确认所提供的安全性保证也很弱（与真正的 PoS 最终确定相比）。

• MEV 重组：混合型共识机制仍保有这样的实际情况——短期重组是可能的，因此为占据近多数或多数的恶意验证者共谋重组区块链来提取 MEV 价值敞开大门。这篇文章更为详尽地对这个论点进行了阐述。
• 交互缺陷：Casper FFG 最终敲定和 LMD GHOST 分叉选择间的“接口”是重要复杂性的来源，导致了很多需要相当复杂的补丁去修复的攻击，还有更多的弱点被时不时地发现。
• 其他协议复杂性：数百行规范被用于维护验证者集合洗牌等机制。

好消息：超大规模的验证者集合因 BLS 聚合变得比想象中更有可能

在过去三年内，BLS 实现的具体效率得到了突飞猛进的提升，同时我们掌握了更多高效地处理组合大量消息和数据的知识。

使用 BLS 支持大量验证者面临着两个主要的瓶颈：

• 最后的验证：验证来自 N 个验证者的签名需要多达 N/2 次 ECADD 来计算群公钥，并需要 N 位（N/8 字节）的位域来存储参与者。实际上，由于 view-merge （视域合并）需要冗余的聚合者，这些数值需要增加多达 16 倍。
• 聚合：将 N 个验证者各自发送的签名组合为一个聚合签名。这需要总共至少 96*N 个字节的带宽来处理，并且需要至少 N 次在 G2 群之上的 ECADD （多于 4 倍计算强度），但分配到各个子网中会更为简单。

实际上，最后的验证扩展能力很强。单次 ECADD 可以在约 500 毫微秒 (ns) 内完成，因此 100 万次 ECADD 将花费约 500 毫秒 (ms)。100 万验证者位域的大小仅为 128 kB。

view-merge 的冗余可能需要每个 slot 验证多达 16 个单独的签名；这将数据存储需求提升到仍然可控的 2 MB（大致等于 EIP-4844 中每个区块 blob 数据的大小上限，以及当前每个区块 calldata 大小上限），同时在最坏情况下 ECADD 运算成本增加约 8 倍（由于巧妙的预计算技巧，不用增加 16 倍）。

这些是最坏情况下的数值；在通常情况下，16 个聚合者的位域是基本一致的，这让多个聚合的主要额外成本得以压缩。

聚合更具挑战性，但也是相当可行的。最新研究大大加深了我们对如何在一个 slot 内聚合大量签名的理解。好消息是，我们有充分的理由相信，每个 slot 处理数十万的签名是可能的，尽管仍需更深入的研究工作来确定和商定最佳解决方案。

这两个事实结合在一起意味着，权衡的结果不再倾向于在基于链和基于 BFT 的 PoS 间进行折衷，而是更接近完全的传统 BFT 路线的解决方案，即在下个区块开始前敲定每个区块。

我们需要解决哪些关键问题以实现单个 slot 最终确定性？

共有三个关键问题：

• 开发确切的共识算法：我们不太能接受 Tendermint 或其他现有的 BFT 算法，因为我们十分看重这一点：即使在大于验证者离线的情况下，区块链仍然能够保持活性（这是传统 BFT 无法提供的）。我们需要添加一个分叉选择规则、怠工惩罚（inactivity leak）和恢复机制来实现这种活性。理想情况下，我们能够获得最佳的安全性：网络同步时，容错率为；当网络不同步时，容错率为。
• 确定最优聚合策略。对于尽可能高的，我们想聚合来自个验证者的签名并将其打包进一个块内，而且节点开销是我们愿意接受的水平。
• 确定验证者的经济模型。尽管聚合和最后的验证这两个步骤有所改进，单个 slot 实现最终确定性的以太坊可能最终能够支持的的验证者数量理论上限比当前的以太坊更小。如果这个数值最终低于欲参与的验证者数量，我们该如何限制参与，以及我们会做出什么样的牺牲？

确切的共识算法会是怎样的？

如上所述，我们想要一个遵循 Casper FFG + LMD GHOST “最终确定链+乐观链”范式的共识算法，在极端条件下，乐观链可以回滚，但最终确定链永远不能回滚。

这需要一个与分叉选择规则和最终确定性工具与现有共识类似的结合，但其中有一个关键的区别：当前，我们通常会同时运行分叉选择规则与最终确定性工具，但在单个 slot 实现最终确定性的世界中，我们会要么运行分叉选择规则，要么运行最终确定性工具：如果小于三分之二的验证者在线并且诚实地工作，那么运行前者；否则，运行后者。

对该算法的具体提案仍在进行中；目前仍未发布正式的成果或文章。

开发一个最优的聚合策略会面临哪些问题？

先让我们看看当前是如何进行聚合的。在单个 slot 内，约有2的14次方个验证者，这些验证者被划分为

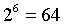个委员会，每个委员会约有

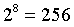个验证者。首先，每个委员会中的验证者在该委员会专用的 p2p 子网中广播他们的签名。每个委员会中有 16 个指定的聚合者，每个聚合者将看到的所有签名合并为一个聚合签名（96 字节 + 256 字位的位域）。指定的聚合者将其聚合签名发布到主子网中。

然后，区块提议者从每个委员会中挑选最佳的（即参与者总余额最大）聚合签名，并将其打包进区块。有了 view merge 分叉选择的补丁，它们还会添加一个包含其他聚合签名的跨斗 (sidecar) 对象；只要每个委员会中至少有一个聚合者是诚实的，就可以保护 view merge 机制免受恶意聚合者的影响。

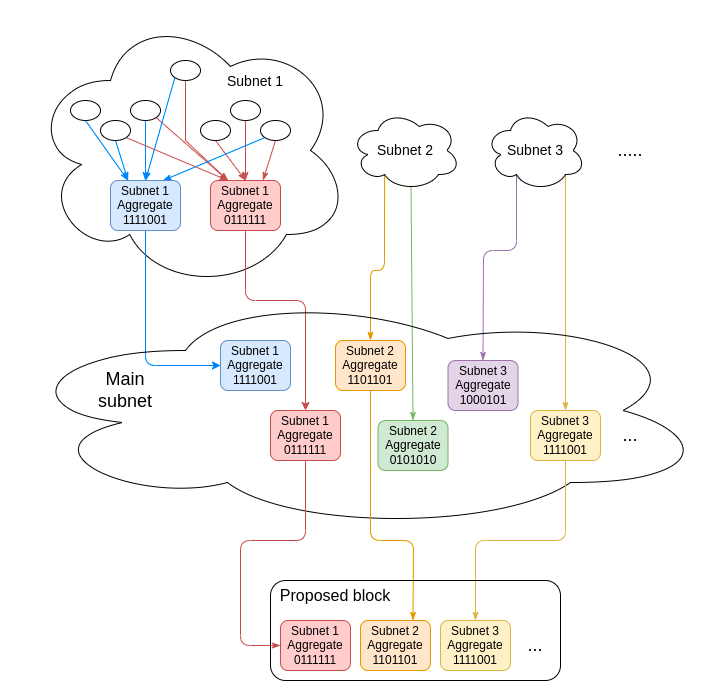
如果我们想把这个模型扩展到单个 slot 实现最终确定性的场景，那么我们需要能够在每个 slot 之内处理所有的2的19次方 (或无论我们有多少) 个验证者。这需要在以下两种取舍中取其一：

• 增加单个委员会的验证者数量或者增加委员会数量，或两者兼而有之，以适应更多的验证者。
• 转向三层聚合，两层委员会的结构。首先，签名先划分成大小为

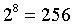的小组进行聚合 ，然后大小为

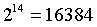的小组，最后是完整的验证者集合。

前者要求更大的 p2p 网络带宽，后者要求接受更高的延迟，更多的 p2p 子网层级带来更高的风险以及额外复杂性来确保 view merge 免受所有层级中的恶意聚合者所影响。

对这两种策略的分析研究在持续进行中。

验证者经济模型存在着哪些问题？

当前，以太坊有着约2的19次方个活跃的验证者（准确来说，在本文撰写时为 445064 个），每个验证者都质押了 32 个ETH。到单个 slot 最终确定性实现时，验证者数量可能会增加到2的20次方甚至更高。

这带来了一个重大问题：如果我们每个 slot 只能处理来自 N 个验证者的签名，但如果有超过 N 个以上的验证者想要参与，那么我们该如何确定谁去谁留？

这是一个重大问题，因为任何方案都将涉及弱化 staking 系统的一个或多个被视为安全保障的特性。

好消息：源于支持自发验证者余额合并的收益

因为单个 slot 最终确定性移除了委员会的概念（甚至 danksharding 也不会使用固定大小的委员会），我们不再需要 32 ETH 的验证者有效余额上限。考虑到 p2p 网络稳定性的因素，我们仍然想要一个更高的上限（例如，2048 ETH），但即便如此，这也意味着本来属于富有用户的大量验证者槽位将会被合并成数量少得多的验证者槽位。

我们可以用 Zipf 定律估计整合富有用户的验证者 slot 的收益：某个拥有特定余额的质押者数量与其余额成反比（因此余额为 100-2000 ETH的质押者数量是余额为 1000-2000 ETH 的质押者数量的 10 倍）。

使用了信标链的早期历史数据，Zipf 定律似乎相当准确地拟合了分布：

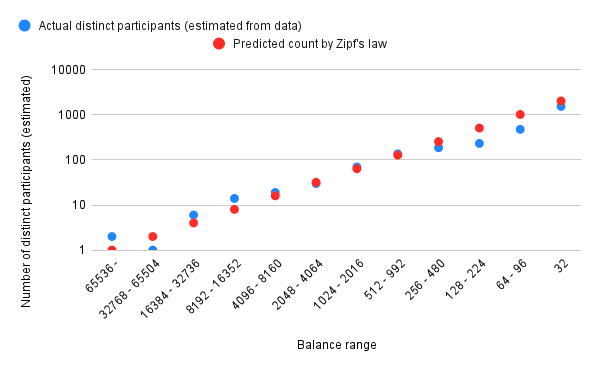
假设符合 Zipf 定律，N个质押者将拥有大约

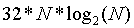个 ETH，那么今天就需要

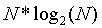 个验证者槽位。把

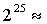3350万 ETH填入该式子，我们可以得到共计 65536 个质押者，在今天的以太坊则需要消耗

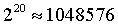个验证者槽位。因此，完全移除有效余额上限让需要处理的验证者槽位数量减少到 65536 个，而维持 2048 ETH 的上限（提升自当前的 32 ETH）只会额外增加约 1000 到 2000 个验证者。只需将聚合性能提升约 2 倍或让负载增加约 2 倍，就能够处理当前情况下的单 slot 最终确定性！

作为一个附带的好处，这也对小型质押者更加公平，因为小型质押者可以质押全部余额而不是一部分（例如，当前拥有 48 ETH的人只能质押其 2/3 的 ETH）。质押奖励将自动被重新质押，即使是小型验证者也能从复利中获益。事实上，出于这个原因，把质押上限提高到 2048 ETH 甚至可能是一个好主意！

然而，我们仍需要处理例外情况：（i）验证者余额分布不再符合 Zipf 定律，或（ii）富有的验证者不打算合并其余额，或（iii）质押了超过 3300 万的 ETH。

我想到了处理这些情况的两种现实策略：超级委员会和设定验证者集合大小上限。

思路 1：超级委员会

不是所有验证者都参与每一轮 Casper FFG，而是只有一个由数万人组成的中型超级委员会参与，让每轮共识都在一个 slot 内发生。

这一技术思路在这篇帖子中首次介绍。这篇帖子更加详细地描述了该思路，但其核心原则很简单：在任何给定的时间，只有一个从完整验证者集合随机抽样得到的中型超级委员会（例如，价值 4 百万 ETH）被激活。每次链达到最终确定性，委员会都会改变，其中多达 25% 的成员会被随机采样的新验证者替换。

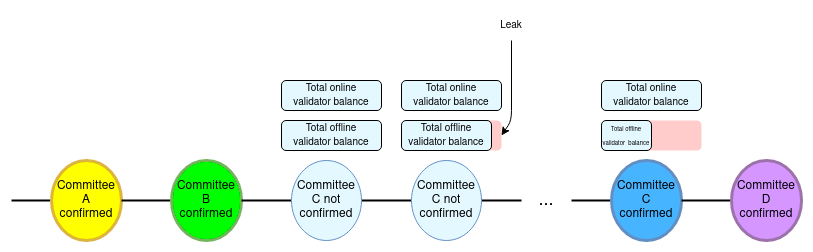
在该策略中，“谁留谁走？”就是：每个人都会逗留一部分时间，而在另一部分时间离开。

超级委员会得有多大？

这个问题可以归结为一个更简单的问题：51% 攻击以太坊需要多少代价？理想情况下，由于攻击被 罚没以及怠工惩罚的 ETH 数量需要大于从攻击中实际获得的收益。攻击的成本甚至应该足够高，从而让那些有强烈外部动机去毁灭这条链的强大攻击者受到威慑或损失惨重。

回答实现这一目标需要多少ETH 这一问题不可避免地要依赖直觉。以下是一些我们可以问的问题：

• 假设以太坊受到 51% 攻击，社区需要花几天时间协调链下治理来恢复，而 X% 的 ETH 被烧毁。X 需要多大才能对以太坊生态产生净效益？
• 假设一个大型交易所被黑客入侵导致损失了数百万的 ETH，攻击者将收益存入并占有超过 51% 的验证者。在被盗资金被完全销毁前，攻击者能够对链进行多少次51%攻击？
• 假设某个 51% 攻击者在短时间内反复重组区块链来捕获所有的 MEV。我们想让攻击者每秒付出什么级别的代价？
• 来自 Justin Drake 的估算表明，当前对比特币进行 spawn-camp 攻击（即持续进行 51% 攻击直到社区改变 PoW 算法）的成本约为 100 亿美元，或比特币市值的 1%。对以太坊进行一次 51% 攻击的成本应该是该水平的多少倍？

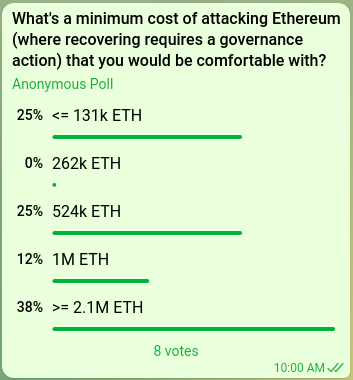以太坊研究员的内部投票

如果我们仅关注不依赖网络延迟的 51% 攻击，100 万枚 ETH 的攻击成本意味着 200 万枚 ETH 规模的超级委员会（约 65536 个验证者）。如果我们还考虑涉及恶意验证者和网络操纵的复杂组合的 34% 攻击，那么规模为 300 万枚 ETH (大约 97,152 个验证者)。

复杂性成本

除了降低攻击成本以外，该方案的另一个主要弱点是复杂性，包括协议复杂性和分析复杂性。特别是：

• 我们需要数百行规范代码来选举超级委员会并进行轮换。
• 富有的验证者会在多个验证者槽位间分配其 ETH 以减少收益波动，因此我们会因提高有效余额上限失去了一些好处。
• 若出现临时性的高手续费或高 MEV，超级委员可能会故意拖延最终确定性的达成来避免被换出，从而可以继续收取手续费和 MEV。

思路2：设置验证者集合规模上限

我们可以试着采用两类设置上限方案中的一种（或两种）：

• 设置 ETH 质押总量上限
• 设置验证者总量上限

每种设置上限的方案都可以选择基于顺序的机制 (堆栈或队列) 或经济模型调节的机制来实现。

基于顺序的机制有着很多问题。要了解其中原因，可以考虑两类基于顺序的策略：

• 保留最旧的验证者（OVS）：如果验证者集合已满，那么其他人无法加入
• 保留最新的验证者（NVS）：如果验证者集合已满， 那么最旧的验证程序将被踢出

这两类都有着严重的问题。OVS 有着转向一个早期质押者盘踞其中的“王朝”的风险，质押者一旦离开，则可能会永远失去再加入的机会。这也会导致每当某个验证者离开都会出现 MEV 拍卖或排着长队以加入验证者集合。另一方面，NVS 可能会引发持久的 MEV 竞拍，这会干扰整条链，因为被踢出的验证者会想立即重新加入，从而与真正的新参与者进行竞争。

通过经济模型设置 ETH 质押总量上限

另一种可选机制是使用经济学模型设置上限：如果存在过多的验证者想参与，那么惩罚所有新旧验证者，直至某些验证者放弃并离开。一个简单的方法是将验证者奖励公式从当前的

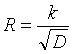更改为形如：

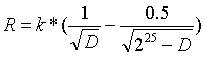
其中R是对表现良好的验证者的奖励（表现不佳的验证者会获得相对较低的奖励），而D是当前活跃验证者的 ETH 总余额。该曲线大致如下：

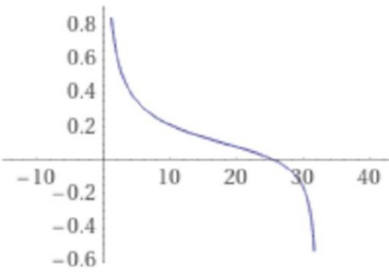
在曲线的左侧，验证者奖励起到与当前机制一致的作用。但是，随着 ETH 质押总量增加到数百万，奖励函数开始加速下降，在约 2500 万 ETH 时，奖励会降至零以下。在优先费用（priority fee）和 MEV 收益足以覆盖其损失的特殊情况下，尽管基本收益为零或负数，验证人可能会愿意继续质押。奖励曲线在2的25次方 ETH（约 3350 万ETH）处趋于负无穷，从而无论外部奖励有多高，验证者集合的大小无法越过该上限。

该方法的优势在于它完全避开动态队列的设计：无论均衡点在哪里，它都能达到均衡；验证者集合大小最终会达到均衡点（在当前条件下，没有更多的验证者想要参与）。

该方法的主要缺点是在曲线右侧附近持续进行阻拦攻击：攻击者可以加入并快速赶出其他验证者。但这是相对其他方案而言的一个小问题，因为它只能在 MEV 异常高的情况下发生，而且这种攻击非常昂贵（需要数百万枚 ETH）。

另一个主要缺点是，它可能使得我们趋于一个大多数验证者都被“边缘化”的未来，大型质押者由于更能容忍收益波动，从而在竞争中会胜过小型质押者。

通过经济模型设置验证者总量上限

通过添加正比于验证者总量的惩罚项，我们可以使用相同的逻辑来设置验证者总量上限。例如，如果我们想要设置的验证者上限为

2的17次方，我们可以这样做：

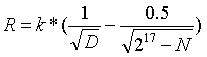
另一种方法是添加浮动最低余额：如果验证者总量超过上限，则将拥有最低余额的验证者踢出。

浮动最低余额会面临一类新型的恶意攻击的挑战：富有的验证者划分他们的质押资金，以便踢走小型验证者（从而增加了他们的奖励R，因为质押总量D减少了）。我们可以通过增加每个验证者槽位的费用来缓解这一问题，并达到这样的目的：在 Zipf 分布下，不值得进行此类攻击。然而，如果不再服从 Zipf 分布，那么仍会留下一个潜在的漏洞。

所有这些提案的一个重要问题是，它们改变了现有安全保证。尤其：

• 超级委员会将攻击链的成本从质押总量的 1/3 降低到约 1 到 2 百万 ETH。
• 通过经济模型设置质押总量或验证者总量上限设计改变 ETH 发行公式，减少质押者的收益，并增加恶意攻击。
• 如果我们添加浮动最低余额，该余额可能会超过 32 ETH，违背了当前任何持有 32 ETH的人都可以参与质押的保证。

仍需仔细考虑以确定社区最能接受哪种权衡。

总结

这里有三个主要问题需要研究：

• 开发具体的共识算法，有限度地将 BFT 共识算法与分叉选择规则结合起来。
• 确定最佳聚合策略，在一个 slot 内聚合尽可能多的验证者签名。
• 确定验证者的经济模型：如果成为验证者的需求超过了系统处理验证者的能力，那么需要回答谁去谁留。

(1) 是一项专业的学术任务，我们了解答案的大致轮廓，主要在于填写细节。也就是说，加快 (1) 并争取尽快提出具体设计方案是一个好主意，因为它会与其他研究领域（如提议者/建造者分离 以及 SSLE）交互。

(2) 也是一项专业任务，尽管很可能不可避免地揉合复杂性/效率上的权衡。(3) 涉及到最为困难的权衡取舍，不仅是技术层面的，也需要社区的参与。

特别感谢 ECN 社区翻译志愿者 @doublespending 对本文的翻译贡献。

责任编辑：MK