Vitalik：如何构建安全的中心化交易所平台？

Vitalik Buterin2022-12-29热度: 21209

短期内，有两种明确的交易所类别：托管型交易所和非托管型交易所。

原文标题：Having a safe CEX: proof of solvency and beyond

原文作者：VitalikButerin

原文来源：vitalik.ca

编译：双花，ETH 中文

特别感谢 Balaji Srinivasan 以及 Coinbase、Kraken 和 Binance 团队的探讨。

每当大型中心化交易所崩溃时，一个常被提及的问题是：我们是否可以利用加密技术来解决这个问题。交易所可以通过创建密码学证明的方式证明其链上持有的资金足以偿付用户，而不仅仅依靠政府牌照、审计员、调查公司治理以及交易所法人背调等「法币」方案。

更有野心的是，交易所可以建立一个未经储户同意无法提取储户资金的系统。我们可以尝试探索「不作恶」有职业素养的 CEX 与「无法作恶」却泄漏隐私的低效链上 DEX 之间的界限。这篇文章将深入探讨让 CEX 更加去信任的历史尝试，与其采用技术的局限性，以及一些依赖 ZK-SNARKs 等先进技术的有力手段。

余额表和 Merkle 树：传统的可偿付证明

交易所试图用密码学来证明自己没有欺骗用户的最早尝试可以追溯到很久以前。2011 年，当时最大的比特币交易所 MtGox 通过发送一笔移动 424,242 个 BTC 到预先公布地址的交易来证明他们拥有该笔资金。2013 年，大家开始讨论如何解决该问题的另一面：证明用户存款的总规模。如果你证明用户的存款等于 X （负债证明 proof of liabilities），并证明拥有 X 个代币的私钥（资产证明 proof of assets），那么就提供了可偿付证明（proof of solvency）：你证明了交易所有足够的资金偿还给储户。

提供存款证明的最简单方法是公布一个列表。每个用户都可以检查他们在列表中的余额，而且任何人都可以检查完整的列表：（i）每项余额都是非负的；（ii）总额是宣称的金额。

当然，这会破坏隐私，所以我们可以稍微改变一下该方案：发布一个 <username, salt), balance> 列表，并私下给用户发送 salt 值。但即使这样也会泄漏余额与其分布。为了保护隐私，我们采用了后续技术：Merkle 树技术。

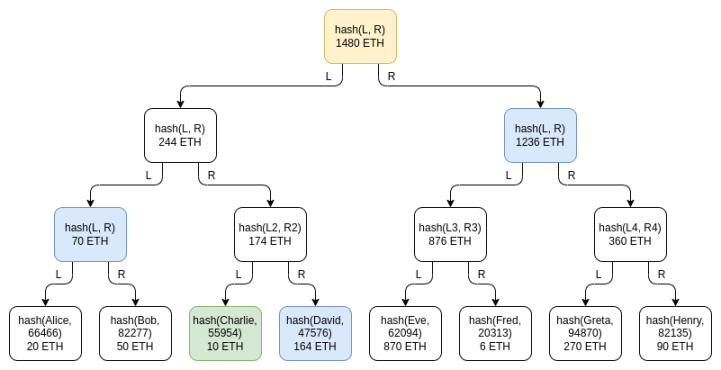
Vitalik

绿色：Charlie 的节点。蓝色：Charlie 收到用于证明的节点。黄色：根节点，向所有人公布

Merkle 树技术会将用户余额表放进 Merkle 总和树。在 Merkle 总和树中，每个节点都是对。底层叶子节点表示各个用户的余额以及用户名的加盐哈希。在每个更高层的节点中，余额是下面两个节点余额的总和，而哈希是下面两个节点的哈希。Merkle 总和证明和 Merkle 证明一样，是一个由叶子节点到根节点路径上所有姐妹节点组成的「分支」。

首先，交易所会向每个用户发送一份其余额的 Merkle 总和证明。然后，用户能够确定其余额作为总额的一部分而被正确地包含。可以在这里找到简单的示例代码。

# The function for computing a parent node given two child nodes

def combine_tree_nodes(L, R):

L_hash, L_balance = L

R_hash, R_balance = R

assert L_balance >= 0 and R_balance >= 0

new_node_hash = hash(

L_hash + L_balance.to_bytes(32, 'big') +

R_hash + R_balance.to_bytes(32, 'big')

)

return (new_node_hash, L_balance + R_balance)

# Builds a full Merkle tree. Stored in flattened form where

# node i is the parent of nodes 2i and 2i+1

def build_merkle_sum_tree(user_table: "List[(username, salt, balance)]"):

tree_size = get_next_power_of_2(len(user_table))

tree = (

[None] * tree_size +

[userdata_to_leaf(*user) for user in user_table] +

[EMPTY_LEAF for _ in range(tree_size - len(user_table))]

)

for i in range(tree_size - 1, 0, -1):

tree[i] = combine_tree_nodes(tree[i*2], tree[i*2+1])

return tree

# Root of a tree is stored at index 1 in the flattened form

def get_root(tree):

return tree[1]

# Gets a proof for a node at a particular index

def get_proof(tree, index):

branch_length = log2(len(tree)) - 1

# ^ = bitwise xor, x ^ 1 = sister node of x

index_in_tree = index + len(tree) // 2

return [tree[(index_in_tree // 2**i) ^ 1] for i in range(branch_length)]

# Verifies a proof (duh)

def verify_proof(username, salt, balance, index, user_table_size, root, proof):

leaf = userdata_to_leaf(username, salt, balance)

branch_length = log2(get_next_power_of_2(user_table_size)) - 1

for i in range(branch_length):

if index & (2**i):

leaf = combine_tree_nodes(proof[i], leaf)

else:

leaf = combine_tree_nodes(leaf, proof[i])

return leaf == root

这种设计下的隐私泄露远低于公开完整的余额表，并可以在每次默克尔根发布时打乱各个分支来进一步降低隐私泄漏风险，但仍存在一些隐私泄露的问题：Charlie 知道某人的余额为 164 ETH，某两个用户余额的总和为 70 ETH，等等。控制多个帐户的攻击者仍能了解交易所用户的大量信息。

该方案的一个重要的微妙之处在于负余额的可能性：如果一个拥有 1390 ETH 用户余额却只有 890 ETH 储备的交易所试图通过在树上某处的一个假账户下添加 -500 ETH 余额来弥补差额，该怎么办？这种可能性实际上并没有破坏该方案，这就是我们特地使用 Merkle 总和树而不是常规 Merkle 树的原因。假设 Henry 是交易所控制的假账户，而且交易所在上面放了 -500 ETH：

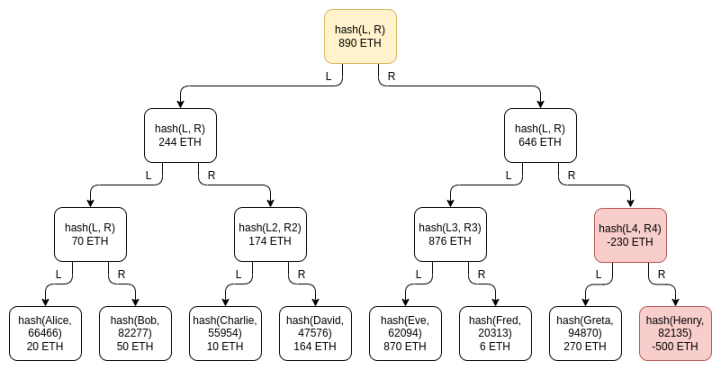
Vitalik

Greta 的验证将不会通过：当交易所将不得不把 Henry 余额为 -500 ETH 的节点的给她时，她会拒绝掉该无效节点。Eve 和 Fred 也会验证失败，因为 Henry 之上的中间节点余额为 -230 ETH，所以该节点也是无效的！为了盗用行为不被发现，交易所只能寄望于树的右半部分没人检查其余额证明。

如果交易所能够挑选出这样的拥有 500 ETH 的用户：他们嫌麻烦不去检查余额证明，或者当他们抱怨未能收到余额证明时，大家并不相信他们，那么交易所就可以蒙混过关。但是，交易所也可以通过将这些用户排除在 Merkle 总和树之外来达到相同的效果。因此，如果仅就负债证明而言，Merkle 树技术基本满足了需求。但它的隐私特性仍不够理想。你可以更巧妙地使用 Merkle 树进行改进，比如把 satoshi 或 wei 作为一个独立的叶子节点。然而，通过使用更先进的技术，还可以做得更好。

使用 ZK-SNARKs 来提高隐私性和健壮性

ZK-SNARKs 是一项强大的技术。ZK-SNARKs 对密码学的意义类似于人工智能：一项足以碾压数十年前为了解决一系列问题而开发的一系列专用技术的通用技术。因此，我们当然可以使用 ZK-SNARKs 极大地简化和改善负债证明协议中的隐私。

我们可以简单地将所有用户的存款放进 Merkle 树（或者更为简单的 KZG 承诺 )，并使用 ZK-SNARK 来证明树中的所有余额都是非负的，并且加起来等于某个声称的值。如果我们添加了一层哈希来保证隐私，那么发给每个用户的 Merkle 分支（或 KZG 证明）将不会泄漏任何其他用户的余额。

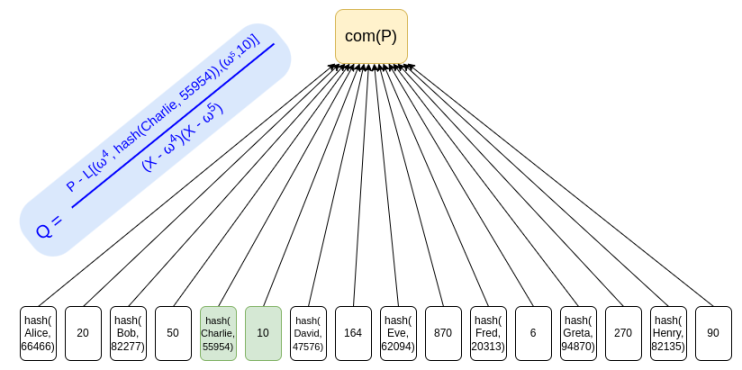
Vitalik

使用 KZG 承诺是避免隐私泄露的一种方法，因为其不需要把「姐妹节点」作为证明提供，并且可以使用简单的 ZK-SNARK 来证明余额的总和，并且每个余额都是非负的。

我们可以通过一个专用的 ZK-SNARK 来证明上述 KZG 中余额的总和及其非负性。这里有一个简单的例子。我们引入了一个辅助多项式 I(x)，其「构建出用户余额的每一位」（为了举例，我们假设余额低于 215），其中每第 16 个位置追踪差额保证，只有当实际总额与宣称总额相等该值才会是 0。如果 z 是一个 128 阶的原根，我们可以证明方程成立：

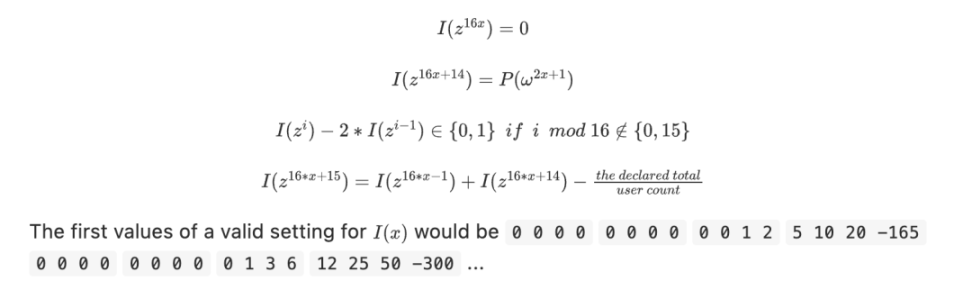
Vitalik

[1] 译者注：对这个多项式等式的解读。

如何把这些等式转换为多项式校并在后续转换为 ZK-SNARK 可以参考我撰写关于 ZK-SNARKs 文章的此处和另外一处。这并不是一个最优的协议，但让这些密码学证明比较好理解！

只需要几个额外的方程式，该约束系统就可以适配更复杂的设定。例如，在杠杆交易系统中，个人用户拥有负余额是可以接受的，但前提是他们需要拥有足够的抵押资产以覆盖其负债。SNARK 可以用于证明这一更为复杂的约束，向用户保证，交易所不能秘密违规豁免某些用户，从而危及用户资产。

长远来看，这种 ZK 负债证明的用处不限于交易所中的用户存款，还可以用于更广泛的贷款场景。任何贷款的人都会将记录放入含该贷款的一个多项式或一棵树中，而根会在链上发布。这将使得任何寻求贷款的人向放款方提供零知识证明，以表明其未获得太多其他贷款。最终，法律上的创新甚至可以使得以这种方式进行承诺的贷款比无承诺的贷款拥有更高的优先级。这与我们在《去中心化社会：寻找 Web3 的灵魂》中讨论的一个想法不谋而合：通过某种形式的「灵魂绑定代币」，使得链上负面信誉的概念成为可能。

资产证明

资产证明最简单的版本是我们上面看到的协议：为了证明您持有 X 个代币，您只需在预定时间移动 X 个代币或在交易中携带「这些资金属于 Binance」的信息。为了避免支付交易手续费，你可以签署一条链下消息。比特币和以太坊都有链下签名信息标准。

这种简单的资产证明技术存在两个实际问题：

冷钱包处理
抵押品重用

出于安全考虑，大多数交易所会将大部分用户资金存储在冷钱包中：在离线的计算机上，交易需要手动签名并携带到互联网上。这种手段是很普遍的：我过去用于存放私人资金的冷钱包放在一台永久离线的计算机上，它会生成包含已签名交易的二维码，然后我会用手机扫描这些二维码。由于资金量庞大，交易所使用的安全协议会更加复杂，经常涉及在多个设备间的多方计算，以进一步降低单设备被黑导致密钥泄露的可能性。在这种背景下，即使是创建一条额外消息来证明对地址的控制也是一项昂贵的操作！

交易所可以采用以下几种方式：

● 维护一些长期使用的公开地址。交易所生成若干地址，仅发布一次每个地址所有权证明，然后重复使用这些地址。这是迄今为止最简单的方案，尽管它在保护安全及隐私上增加了一些限制。

● 持有很多地址，然后随机证明几个地址。交易所持有很多地址，甚至可能每个地址只用一次，并在单次交易后不再使用。在这种情况下，交易所需要有一个协议，不时地随机选择一些地址，交易所必须「打开」以证明所有权。一些交易所已通过审计员进行了类似的操作，但原则上，这种技术可以转化为完全自动化的程序。

● 更复杂的 ZKP 方式。例如，交易所可以将其所有地址设置 1/2 多签，这些地址的其中一份密钥各不相同，而另一份相同的密钥是以某种复杂但安全的方式（如，12/16 多签）存储起来重要的紧急备份盲版。为了保护隐私并避免泄漏其全部地址，交易所甚至可以在区块链上运行零知识证明以证明该格式链上地址的总余额。

另一个主要问题是防止抵押品重用。彼此间来回转移抵押品以证明储备金对交易所而言通常很容易办到，这使得实际上没有偿付能力的情况下蒙混过关。理想情况下，可偿付证明应该实时完成，并在每个区块后更新证明。如果不切实际的话，那么下一个最好的办法就是交易所间协调出一个固定的时间进行证明，例如在 UTC 时间每周二下午 2 点证明储备。

最后一个问题是：能在法定货币上做资产证明吗？交易所不仅持有加密货币，还持有银行系统内的法币。在这方面，回答是肯定的，但这样的程序将不可避免地依赖于「法币」信任模型：银行自身可以证明余额，审计人员可以证明资产负债表等。鉴于法币不能通过密码学验证，这是在该框架内的最佳方案，仍然值得一做。

另一种方法是将实体 A 和实体 B 分离开来，A 负责运行交易所并且处理 USDC 这种由某种资产背书的稳定币；而 B 负责在加密货币和传统银行系统之间处理现金流入和流出的过程，在这个案例中 B 即是 USDC 本身。由于 USDC 的「负债」只是链上的 ERC20 代币，所以负债证明是可以「轻易」获得的，而我们只需处理资产证明的问题。

Plasma 和 validiums: 我们可以实现非托管 CEX 吗？

假设我们想更进一步：我们不想仅仅证明交易所有足够资金偿还其用户。相反，我们想彻底防止交易盗用用户的资金。

在这上第一个尝鲜的是 Plasma，这是一种 2017 年和 2018 年在以太坊研究界流行的扩容解决方案。Plasma 的工作原理是将余额拆分为一组独立的「代币」，每个代币都会分配一个索引，并放到 Plasma 区块的 Merkle 树中的特定位置上。要进行有效的代币转移，需要将交易放到树中的正确位置上，而树根会被发布到链上。

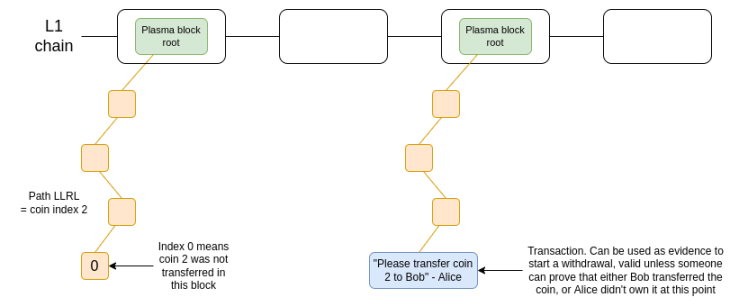
Vitalik

Plasma 的一个版本的极简图。代币被保存在智能合约中，该合约在取款时会强制执行 Plasma 协议的规则。

OmiseGo 试图基于此协议创建一个去中心化交易所，但从那时起，他们就转向去做其他事了——就这而言，Plasma Group 也是如此，他们去做了 optimistic rollup 项目 Optimism。

2018 年对 Plasma 的局限性（如，证明代币碎片整理）的探讨让大家从根本上怀疑 Plasma 的可行性。自 2018 年对 Plasma 的探讨达到顶峰以来，ZK-SNARKs 在扩容相关用例上变得愈加可行，正如我们上面所说的，ZK-SNARKs 改变了一切。

Plasma 更新的版本是 Starkware 称为 validium 的方案：除了数据被保存在链下以外，基本上与 ZK-rollup 相同。该构造适用于许多用例，可以想象其适用于任何中心化服务器需要证明其正确执行代码的场景。在 validium 中，运营方无法窃取资金，但根据具体的实现细节，如果运营方消失，一些用户资金可能会被卡住。

现在看来一切很棒：CEX 和 DEX 远非二选一，事实证明，其中有一系列的选择，包含各种形式的混合中心化，在那里你能获得一些好处，比如效率，但仍有很多密码学保障，可以防止中心化运营方的大部分形式的恶意行为。

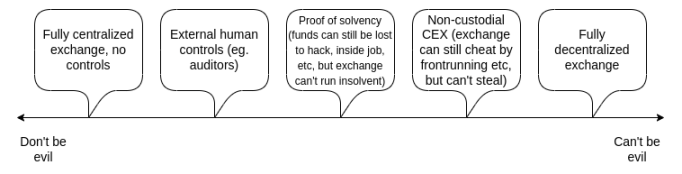
Vitalik

然而，余下的基本问题也值得思考：如何处理用户错误。到目前为止，最重要的错误类型是：如果用户忘记了密码、丢失了设备、被黑或无法访问其帐户，那该怎么办？

交易所可以解决这个问题：首先利用电子邮件恢复，如果连这都失败了，再通过 KYC 进行更复杂的恢复。但若要解决这些问题，交易所需要真正控制这些代币。为了能够合理地恢复用户资金，交易所需要拥有同样可用于无故窃取用户资金的权力。这是一个不可避免的权衡。

理想的长期解决方案是依靠自我托管，用户在未来可以方便地使用诸如多签及社交恢复钱包等技术来帮助处理紧急情况。而短期内，有两种明显的替代方案，有着不同的成本和收益：

Vitalik

另一个重要问题是对跨链支持：交易所需要支持很多不同的链，诸如 Plasma 和 validiums 等系统需要用不同的语言编写代码以支持不同的平台，并且在当前形式下无法在一些平台（尤其是比特币）上实现，这有望通过技术升级和标准化来解决；然而，从短期来看，这是如今托管型交易所保持托管模式的另一个原因。

结论：展望未来更好的交易所

短期内，有两种明确的交易所类别：托管型交易所和非托管型交易所。如今，后一类即像 Uniswap 那样的 DEX，未来我们可能还会看到受密码学约束的 CEX，其中用户资金会以类似 validium 智能合约的方式持有。我们也可能会看到半托管型交易所，其中我们信任其对法币而非加密货币的处理。

这两种类型的交易所将继续存在，而提高托管型交易所安全性的向后兼容最简单方法是增加储备证明。这包括资产证明和负债证明的结合。为两者都设计出优秀的协议仍存在着一些挑战，但我们能够且应当推动两类技术的齐头并进，并尽可能开源软件和程序，以便所有交易所都能获益。

从长远来看，我希望我们向着所有交易所皆为非托管的方向发展，至少在加密货币上如此。钱包恢复将会存在，可能需要为小额资金的新用户和出于法律因素需要此类安排的机构提供高度中心化的恢复选项，但这可以在钱包层而非交易所内部完成。在法币方面，传统银行系统和加密货币生态系统之间的移动可以通过 USDC 等资产背书稳定币原生的资金进出流程完成。然而，我们仍有很长的路要走。