注：原文来自@k63jpx发布长推。

1）Curve TriCrypto-NG Pool

我觉得要深入理解curve的triCrypto-ng的难度/重要性，需要从TriCrypto的算法开始。 不管是curve算法，还是TriCrypto的算法，本质上都是在求解一个非线形方程。

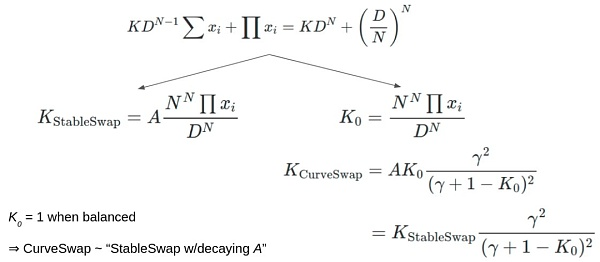
2）Curve TriCrypto-NG Pool

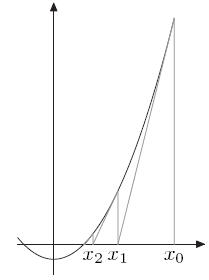
而求解这个非线形方程， 常用的方法是采用牛顿迭代法： 如下图所示，不断在xi点做切线，其与横轴交点横坐标得x{i+1},通过这种不断迭代的方式逼近函数零点，从而得到y值。

3）Curve TriCrypto-NG Pool

curve的gas消耗巨头是因为，它需要在合约上进行求解非线形方程。

这里涉及到两个函数：get_D，get_Y。这里都需要进行255次循环，每次循环都是算出最新的梯度后的切线方程，得到最新的D和Y值。 直到收敛为止。

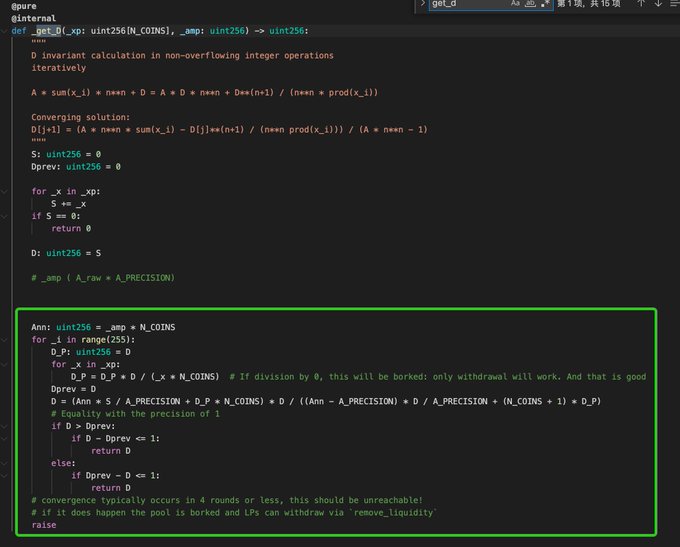
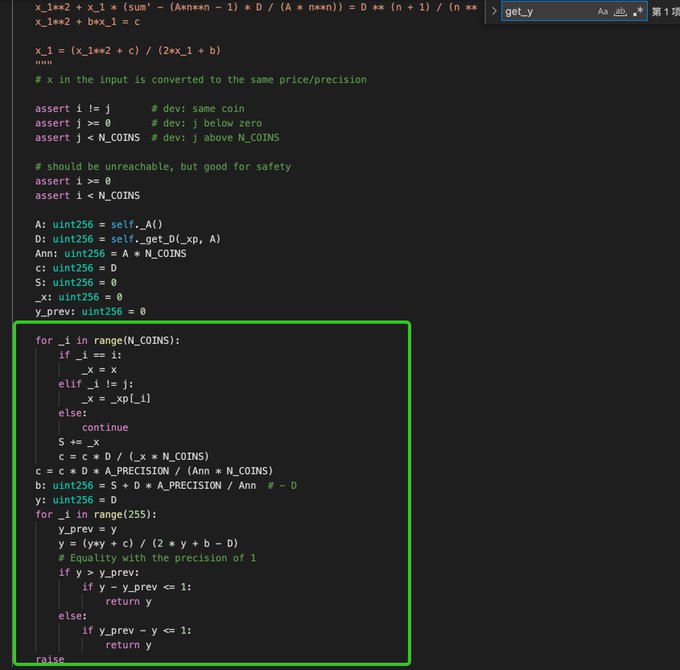
4）Curve TriCrypto-NG Pool

所以，TNG的核心就是：如何在数学上进行优化，更快地求解非线性方程。 这里提出了两个方法来替代原有的get_D和get_y： newton_D 和 newton_Y。

5）Curve TriCrypto-NG Pool

对于求解D值，TNG摒弃了牛顿迭代，采用了Halley 方法进行求根。 “數值分析中，Halley方法是一種求根算法，用於計算具有連續二階導數的一個實變量的函數。它以其發明者愛德蒙·哈雷（Edmond Halley）的名字命名。”

6）Curve TriCrypto-NG Pool

这里我们可以看到，我们只需要知道一阶取导，二阶取导，和函数的f(x）值，只要函数满足三阶可导： 我们可以轻松计算F(x+1)。碰巧的是，tricrypto最终的拟合曲线就是三阶可导。 所以，这里采用Halley's method用来求解，可以优化求解D值使用牛顿迭代法的弊端。

7）Curve TriCrypto-NG Pool

至于y值，curver提出了一种新的找到新y值的方法。我们也不使用牛顿法，因为它是一个迭代过程，只能给出近似解，而是推导出一个新y的精确公式。 采用更容易求解的逼近解，来替代牛顿迭代，从而极大地降低gas。

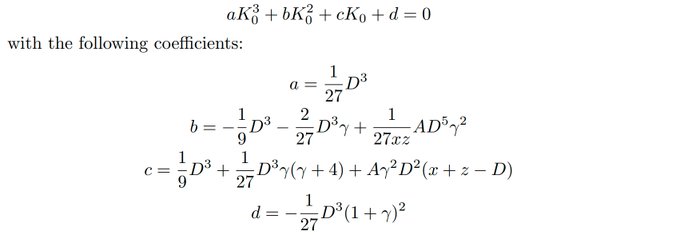
7）Curve TriCrypto-NG Pool 关键

1. 利用Halley's method来直接求解三阶可导的非线形方程，直接得出f(x+1)，从而摒弃效率低下的牛顿迭代法。

2. 基于Halley's method得出的D值，采用超高效的近似值（不需要迭代）来直接计算get_y，从而摒弃效率低下的牛顿迭代法。 从而极大的降低了gas。

8）Curve TriCrypto-NG Pool

我觉得这个非常非常牛逼，赶超uni V3指日可待。 emm，我今天竭尽了全力让DEX组把接入TNG Pool列为T0优先级。我认为以后聚合器的大部分流量都会走TNG Pool。 但希望我这个小小的底层码农能自上而下推得动吧～～ 我是尽力了～ @taowang1 @mrblocktw @CurveFi_Asia

9）Curve TriCrypto-NG Pool的重要性

关于TNG的重要性@DeFi_Cheetah在这篇影响力非常大的推文上分析了

https://twitter.com/DeFi_Cheetah/status/1653581567774855168…

1. 解决了curve算法历史悠久的gas昂贵的问题，从而在以太坊上可以胜出uniV3，从而进一步蚕食AMM的市场，从而提高veCrv的利润。

2. 降低crvUsd使用LLAMMA（AMM）清算成本。

10）Curve TriCrypto-NG Pool

我几乎把市面上的AMM协议全部接了个遍。我可以给出的结论就是：目前几乎没有dex还会继续优化/创新的算法。这就是为什么我深入研究了之后感觉到震惊。

例如：非常流行的就是ve(3,3)的fork，大家都只是在激励上继续摸索；再例如：uniswap甚至直接做nft market去了。

11）总结

当然，目前curve还有蛮多问题的，社区上还可以继续吸收 一些：“更牛逼的前端工程师”，“后端架构师”，从而提升用户体验。（或者直接外包给大厂吧。

但，目前遇到的问题，我觉得这些都是可以解决的。

想了很久为什么如此相信curve，可能是仅仅因为相信数学吧。