注：本文来自@Hill79025920 推特，其是@SevenXVentures研究员，原推文内容由MarsBit整理如下：

证明方案是ZK协议安全假设的基本组成部分。

@srinathtv简洁的解释是得到小于50个赞是一种犯罪。这是我在一个帖子上的尝试，可以帮助更多的人通过添加上下文、解释、比较和优缺点来理解它。

https：//twitter.com/srinathtv/status/1649150174059724801

在ZK证明系统中，涉及三个实体：设置者、证明者和验证者。不同的证明方案可以以不同的方式影响它们的行为，从而影响效率、安全性和整体系统性能。

setup阶段为ZK系统生成必要的参数和公钥。证明方案在复杂性、计算、通信以及是否可信方面影响setup阶段。

证明者在不泄露秘密输入的情况下生成证明。证明方案会影响证明者的计算时间、内存需求和证明大小，从而影响通信和存储需求。

验证者检查证明的有效性。证明方案会影响验证时间、内存需求以及对证明的查询的数量和复杂性。

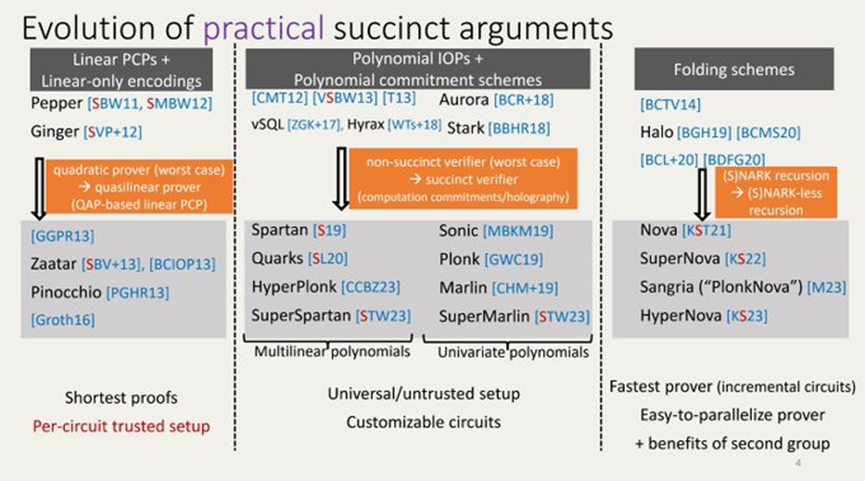
@srinathtv 提供了对三种不同类型的证明方案的概述。

线性 PCP + 线性编码：

-利用线性概率可检验证明(PCP)和线性运算

-提供强大的零知识属性

-生成最短证明

-需要一个可信的设置

-之前的改进主要集中在减少证明者的时间

线性PCP是一种证明系统，在这种系统中，验证者通过查询少量证明来检查语句的有效性。术语“线性”是指验证者的查询是证明的线性函数。

纯线性编码是一种隐藏信息的加密技术，只允许对隐藏的数据进行线性操作。这确保了数据隐私，同时允许执行某些计算。

多项式IOPs +多项式承诺方案：

-利用代数结构

-通常比基于线性PCP的系统更高效

-支持通用/不受信任设置

-允许定制电路

-之前的改进主要集中在提高验证者的效率上

多项式交互Oracle证明(IOPs)是证明系统，证明者和验证者在多轮中交换消息。证明者生成预言(对多项式的承诺)并将其提供给验证者。

验证者在特定点查询预言机，证明者用相应的多项式计算来响应。多项式承诺方案提交一个多项式而不透露多项式本身的信息。

与线性pcp +纯线性编码相比，效率的提高来自：

- 更好地使用代数结构

- 更高效的证明生成/验证

- 压缩多项式表示

- 批量验证技术

然而，多项式IOPs +多项式承诺方案有缺点：

-更复杂的设计和实现

-特殊用途的加密假设

-不同的性能权衡，例如，并行性

折叠方案：

-允许递归证明组合

-支持证明嵌套，以提高效率和可扩展性

-快速，易于并行的证明

-之前的改进主要集中在构建递归SNARKs

递归证明组合导致紧凑的证明历史，减少了对验证者的计算和内存需求。这在区块链等应用程序中特别有用。

证明聚合减少了最终证明的大小和验证次数，但对证明者来说，生成这样的证明可能需要更多的计算量。

多项式IOPs +多项式承诺方案的效率提升来自：

-递归证明组合

-证明聚合

-改进的可扩展性

-更快的验证时间

折叠方案的潜在缺点：

-更复杂的设计和实现

-量身定制的加密假设

-增加证明时间和内存开销

-适用性可能因用例而异

总而言之，线性PCP+纯线性编码提供了强大的零知识特性和最短的证明，但与其他类别相比，它们需要一个可信的设置，并且在效率上有限制。

多项式IOPs +多项式承诺方案比线性PCP +纯线性编码提供了显着的效率改进，具有更有效的证明生成和验证过程，但它们在设计和实现上可能更复杂。

由于递归证明组合，折叠方案在效率和可扩展性方面表现出色，这在区块链应用中特别有用。然而，证明程序的时间和内存开销可能会增加，并且它们的适用性可能因用例而异。

我们希望这篇文章提供了一个有用的和信息丰富的概述，介绍了不同类别的证明方案，以及它们对零知识证明系统中的设置、证明者和验证者的影响。