TL;DR

• SNARK 的构建流程是什么样的？
• 待证明的问题-算术电路-R1CS-多项式
• 为什么最终要转换成多项式？
• 因为多项式的特性有效的缩短了验证时间，实现了简洁性。
• 是如何实现零知识的？
• 简单来说，就是在推导多项式的过程中，多选取两个随机数，以此推导出的多项式能让验证者无法从中获取原多项式的系数，即证明者的秘密输入，以此实现 ZK。
• 怎么实现非交互？
• 在证明开始前，引入了一个第三方，即可信设置，将原本验证者挑选随机数的任务交给了可信设置，从而实现验证者和证明者之间的非交互。

ZK 技术近两年在 Web3 领域备受关注。从 Rollup 开始，越来越多不同赛道的项目都开始尝试使用 ZK 技术。在这之中，SNARK 和 STARK 是大家最常听到的两个名词，为了后期更好地理解ZK技术的应用，本文将从非技术的角度简化阐述 SNARK 的证明逻辑，然后会以 Scroll 的 zk Rollup 为例来说明 zk 证明系统的运行。

文章旨在阐述基本逻辑，便于阅读，会尽量避免术语使用，且不会深入探讨数学转换等细节，如有疏漏，敬请谅解。

2012年1月，加州大学伯克利分校教授 Alessandro Chiesa 与人合作撰写了 SNARK 的论文，提出了术语 zk-SNARK。

zk-SNARK，全称 Zero-Knowledge-Succinct Non-Interactive Argument of Knowledge，是使用了 ZK技术的一种证明系统。需要注意的是，SNARK 是一类方案的名称，有很多不同的组合方法都可以实现 SNARK。

• 零知识（Zero-Knowledge）：只有证明者知道的内容将会被隐藏，除了证明者，其他任何人都无法看到。
• 简短（Succinct）：生成的证明小，验证时间快。
• 非交互性（Non-Interactive）：证明者和验证者之间交互很少，甚至没有。
• 论证（Argument）：验证者的验证只对计算能力受限的证明者有效，因为拥有超强计算能力的证明者可以伪造证明，也就是说，系统具备计算可靠性。
• 知识（Knowledge）：证明者只有知道一些验证者不知道的信息才能计算出证明。

zk-SNARK 要解决的是“计算验证问题”，即验证者能否在不知道证明者隐私的情况下，高效地验证计算结果。

下面将以 zk-SNARK 的简化版构建流程来说明该系统是如何结合零知识达到高效验证的。

zk-SNARK 的构建

将待证明问题转化为多项式

简单来说，SNARK 的思路是将证明陈述是否成立转换成证明多项式等式是否成立。

整个转换过程：待求证的问题➡算术电路➡R1CS➡多项式➡多项式之间的转换

待求证的问题➡算术电路

要通过计算证明一个问题是否为真，首先就要将待证明的问题转化成一个计算问题，而任何计算都可以描述为一个算术电路。

算术电路通常由常数、“加法门”、“乘法门”组成，通过门的叠加，我们可以构建出复杂的多项式。

上图中的算术电路构建的多项式为：（Inp1+Inp2）*（-1）= Output

现实中的问题要转为算术电路极其复杂，我们可以将之简单理解为：输入一些内容，内容经过电路转化，最终输出一个结果。即：

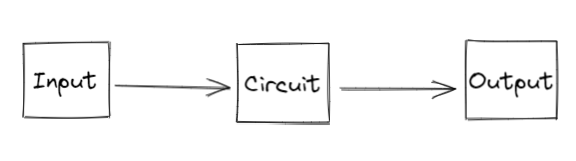
基于算术电路的概念，我们构造一个用于生成证明的算术电路，即：

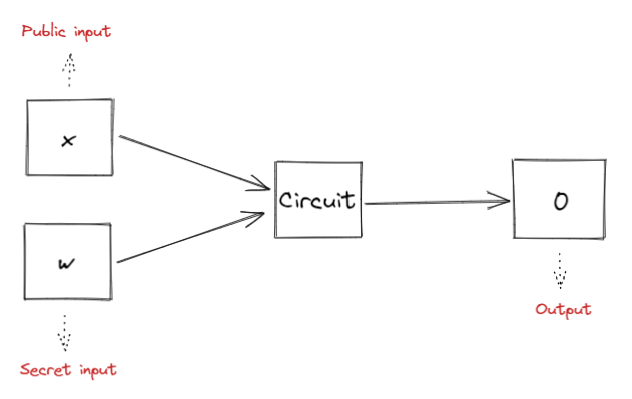
该电路中包含了两组输入，公开输入 x 和秘密输入w。公开输入x意味该内容是待证明问题的固定值，验证者和证明者都知晓，秘密输入 w 则意味着该内容只有证明者知晓。

我们构建的算术电路为 C( x, w ) = 0，即通过电路输入x与w，最终的输出结果为0。证明者和验证者知道电路输出为0，且公有输入为x的情况下，证明者需要证明自己知道秘密输入 w。

算术电路➡R1CS

我们最终需要一个多项式，但算术电路不能直接转化为多项式，需要 R1CS 作为二者间的媒介，故先将算术电路转换为 R1CS。

R1CS，全名为 Rank-1 Constraints System（一阶约束系统），是一种描述电路的语言，本质上是一种矩阵向量方程。具体来说，R1CS 是由三个向量 (a,b,c) 组成的序列，R1CS 的解是一个向量 s，其中 s 必须满足方程：

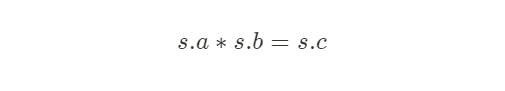
其中 . 代表内积运算。

此间具体的数学转换可以参见 Vatalik：Quadratic Arithmetic Programs: from Zero to Hero

我们只需要知道，R1CS 的作用是对算术电路中的每个门的描述进行限定，使得每个门之间的向量满足以上关系。

R1CS➡多项式

在得到 R1CS 这个媒介后，我们就可以将其等价转换成多项式。

矩阵和多项式之间可以进行如下图所示的等价转换：

多项式

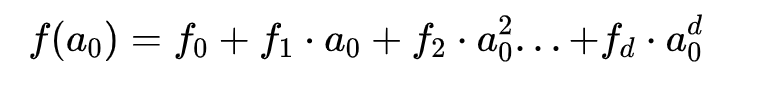
转化为矩阵

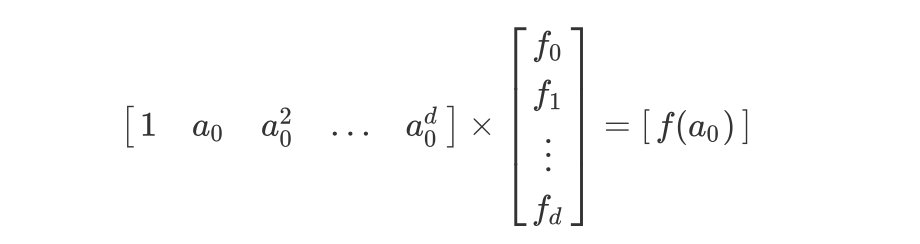
根据上述等价转换的性质，对于满足 R1CS 的矩阵，我们可以使用拉格朗日插值法，还原出多项式每一项系数，基于这个关系，我们可以将 R1CS 矩阵推导为多项式关系，即：

注：A, B, C分别代表一个多项式

一个多项式对应我们想要证明的问题所对应的一个R1CS矩阵约束，通过以上转化，我们可以知道，多项式之间满足以上关系，就说明我们的R1CS矩阵是正确的，从而说明证明者在算术电路中的秘密输入也是正确的。

到这我们的问题就简化为：验证者随机挑选一个数 x，让证明者证明 A(x) * B(x)=C(x) 成立，如果成立，说明证明者的秘密输入正确。

多项式之间的转换

复杂的算术电路中，有成千上万个门，我们需要对每个门验证其是否满足R1CS约束。换句话说，我们需要验证数次 A(x) * B(x)=C(x) 等式成立，但是逐次单独验证的效率太低，如何能做到一次性验证所有门的约束的正确性？

为了方便理解，我们引入一个 P(x)，令 P(x) = A(x) * B(x) – C(x)

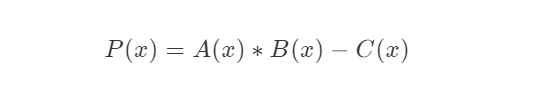我们知道，任意的一个多项式只要它有解，就可以将它分解成线性多项式。故我们将 P(x) 拆分为 F(x) 和 H(x)，即：

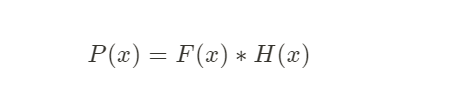然后将 F(x) 公开，这就意味着存在一个 H(x) = P(x)/F(x) ，从而我们要验证的多项式最终转变为 ：

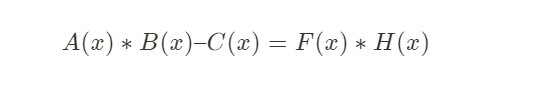A(x) * B(x) – C(x)：包含多项式的系数，只有证明者知，即秘密输入。

F(x) ：一个公开的多项式，验证者和证明者皆知，即公开输入。

H(x) ：证明者通过计算得知，验证者不可知。

而最终要证明的问题为：多项式等式 A(x) * B(x) – C(x) = F(x) * H(x)，在所有x上都成立。

现在只需要验证一次多项式就可以验证所有约束是否满足矩阵关系。

到这里我们就完成了将待证明的问题转化成只需要验证一次的多项式，实现了系统的简洁性。

但是这个实现的简洁性是让验证者的验证时间缩短，那证明大小呢？

简单来说，在证明协议中，使用的是 Merkle 树的结构，这有效的降低了证明的大小。

整个转换过程完成以后，自然而然的会产生两个问题：

• 为什么要转换成多项式？
• 因为多项式实现了证明的简洁性。零知识证明的问题就是验证计算满足多个约束的问题，而多项式可以一个点验证多个约束。换句话说，验证者本来要验证 n 次才能确认的问题，现在只需要验证一次就能极大概率地确认证明的正确性。
• 为什么验证多项式上的一个点，就能确定两个多项式 A(x) * B(x) – C(x )= F(x) * H(x) 成立？
• 这是由多项式的特性决定的，即：一个多项式在任意点的计算结果都可以看做是其唯一身份的表示。对于两个多项式，它们只会在有限的点上相交。

对于上述的两个 d 阶多项式：A(x) * B(x) – C(x) 和 F(x) * H(x)，如果它们不相等，它们最多只会在d 个点上相交，也就是在 d 个点上的解相同。

完成了多项式的转换，我们就要进入多项式证明阶段。

证明多项式成立

为了便于阐述，我们采用多项式 P(x) = F(x) * H(x)。

现在，证明者要证明的问题是：在所有 x 上，P(x) = F(x) * H(x)。

证明者和验证者对以上多项式的验证过程如下：

• 验证者选择随机挑战点 x，假设 x = s；
• 证明者收到 s 后，计算 P(s) 和 H(s)，并把这两个值给验证者；
• 验证者先计算 F(s)，再计算 F(s) * H(s)，并判断 F(s) * H(s) = P(s) 是否成立，若成立则验证通过。

但是我们仔细思考就会发现以上流程存在一些问题：

• 证明者能够知道整个等式的信息，如果收到随机点 s，他能计算出 F(s)，然后构造出一对假的 P(x) 和 H(x)，使得P(s) = F(s) * H(s) ，以此欺骗验证者。
• 证明者不使用验证者给出的 s 计算 F(s) 和 H(s)，而是用其他值计算，以此欺骗验证者。
• 验证者收到的值是由公共输入和证明者的隐私输入一起计算出来的，如果验证者算力极大，可以破解证明者的隐私输入。

针对上述问题，我们进行以下优化：

• 验证者在选取了随机点 s 后，对 s 进行同态加密，同态加密意味着加密后计算的解=计算后加密的解；在这种加密形式下，证明者能够计算出解，但不能构造假的 P(x) 和 H(x)。
• 在验证者选择挑战点 s 时，再选取一个随机参数 λ，额外生成一个 s 和 λ 之间的线性关系。验证者把同态加密后的 s 和 λ 都发给证明者。待证明者将证明发回，验证者除了验证证明是否为真，还需要验证随机参数λ 与 s 之间的关系。
• 针对验证者可破解秘密输入的问题，我们就可以引入 ZK。纵览整个证明，我们可以发现在验证过程中，证明者发给验证者的只有计算出的多项式的值，验证者可以通过值倒推出多项式的系数，即证明者的秘密输入。为了防止验证者倒推，我们可以从 R1CS 推出多项式 A、B、C 的时候，多选取两个随机数并增加一组取值，这样还原出来的多项式比原来的多项式多1阶，从而让验证者无法从加密后的多项式中获取原多项式的信息，以此实现 ZK。

优化以后我们发现证明系统依旧需要验证者和证明者之间进行交互，如何才能实现非交互？

实现非交互

为了实现非交互，SNARK 引入了可信设置（Setup）。

换句话说，在证明开始前，将原本属于验证者的选择随机挑战点的权力交给一个可信的第三方，第三方选择了随机参数 λ 后，将加密后的 λ 放在 R1CS 电路中，以此生成 CRS（Common Reference String，公共参考字串）。验证方能从 CRS 中获取属于自己的 Sv，证明方能从 CRS 中获取属于自己的 Sp。

需要注意的是，λ 在生成 Sv 和 Sp 后，需要被销毁，若 λ 被泄露，可能被用来通过虚假验证伪造交易。

zk-SNARK 工作流程

在明白 SNARK 的构建流程后，基于我们构造的可生成证明的算术电路，zk-SNARK 的证明流程如下：

• Setup:(C circuit, λ)= (Sv, Sp)
• 通过电路 C 和随机参数 λ ，生成后续证明者和验证者使用的随机参数 Sv、Sp。
• Prove(Sp,x,w) = Π
• 证明者通过随机参数 Sp，公共输入 x，秘密输入 w，计算出证明 Π。
• Verify(Sv,x,Π) == (∃ w s.t. C(x,w))
• 验证者通过随机参数 Sv，公共输入 x 和证明 Π 来验证是否存在 C（x,w）=0。同时，验证证明是否是通过电路 C 计算得出。

到此，我们就完成了整个 zk-SNARK 的讲解，下面来看看实际运用的案例。

案例：以 Scroll 的 zk Rollup 为例

证明系统的作用是让证明者说服验证者相信一件事；

对于 zk 证明系统而言，是要让验证者相信由 zk 算法计算出的 Zero-Knowledge Proof（零知识证明）为真。

我们以 Scroll 的 zk Rollup 为例来说明 zk 证明系统的运行。

Rollup 是指链下计算，链上验证。对 zk Rollup 而言，交易在链下执行后，证明者需要对交易执行后产生的新的状态根生成 zk 证明，再将证明传到 L1 Rollup 合约进行链上验证。

需要注意的是，在 zk Rollup 中存在两类区块：

• L1 Rollup 区块：提交到以太坊的区块
• L2 区块：用户在 L2 上提交的交易打包而成的区块

以下是 Scroll 的 zk Rollup 的工作流程：

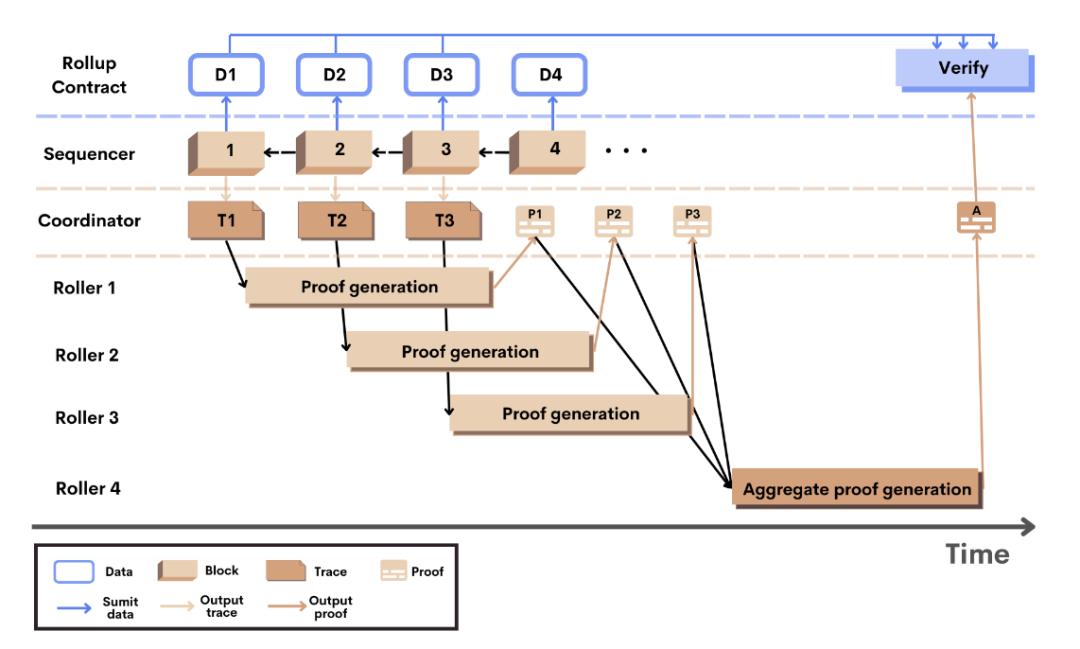
• 用户在 L2 发起交易，Sequencer 检索到交易，在链下执行交易并生成 L2 区块和新的状态根；同时将交易数据和新的状态根提交给以太坊上的 Rollup 合约（提交交易数据是为了实现数据可用性）；
• 当L2区块生成时，Coordinator 会从 Sequencer 那收到该区块的执行轨迹，然后将该轨迹随机分配给任意一个 Roller；
• Roller 将接收到的执行轨迹转换为电路，且为每个电路生成有效性证明，然后将该证明发回给 Coordinator；
• 每生成 k 个 L2块，Coordinator 就会发送一个聚合任务给另一个 Roller，以将 k 个块的证明聚合为单个聚合证明；
• Coordinator 将单个聚合证明提交给 Rollup 合约，Rollup 合约结合之前提交的状态根和交易数据一起验证聚合证明，验证通过则相应的区块就被视为在 Scroll 上最终确定。

从以上流程可以看到，Roller 是该系统中的证明者，Rollup 合约是验证者。Roller 对在链下执行的交易生成一个 zk 证明；Rollup 合约验证该证明，若验证通过，Rollup 合约就会直接采纳提交的状态根作为自己新状态根。

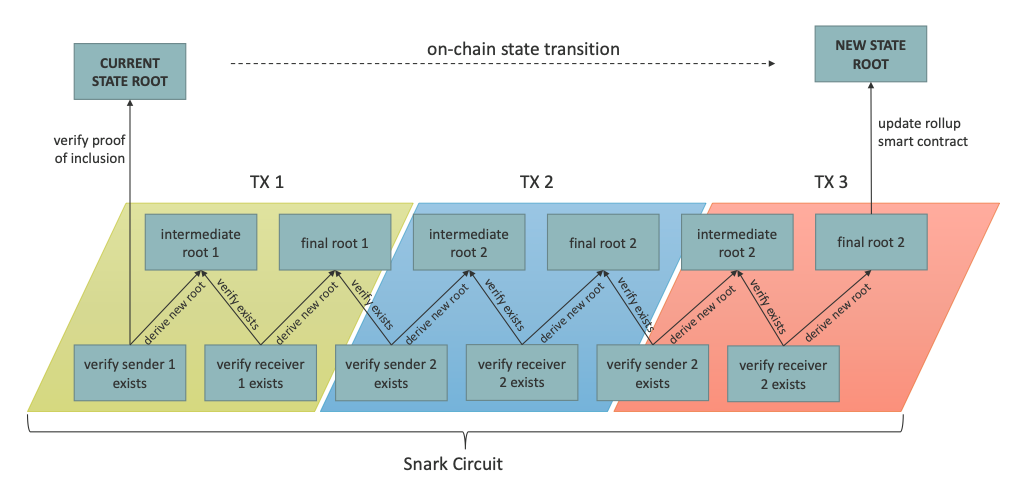
参考

1. Why and How zk-SNARK Works: Definitive Explanation
2. 彻底读懂零知识证明及其实现方法：解析 zk-SNARK
3. 零知识证明引论（三）