PPT 链接: https://img.foresightnews.pro/file/ProofRecursion.pdf

大家下午好, 欢迎来到zkDay Tech Talk。

我叫Maggie，我是 Foresight Ventures 的技术总监。

我很高兴 Dr. Cathie 作为我们这个话题的共同演讲者。Dr. Cathie 是以太坊基金会Privacy & Scaling Explorations团队的 ZKML 研究员。

我们很高兴向您介绍一个前沿主题：“证明递归及其在 ZKML 中的应用。”

如今，证明递归几乎是零知识证明证明庞大复杂程序的唯一方法。 此外，ZKML 将可验证的AI引入区块链。

现在，我想先简要介绍一下我们公司。

• Foresight Ventures 是一家以研究驱动的专注于区块链技术与加密行业的投资机构。我们的产品矩阵包括几个关键组成部分。
• 首先，Foresight News 是亚太地区最大的多语种web3媒体平台。
• 其次，我们运营着 Foresight X，Foresight X是我们的加速器，目前同步在巴黎举办hacker house活动。
• 最后，我们拥有蓬勃发展的全球开发者社区 OpenBuild。

如果您想了解更多关于我们的信息，请随时访问我们的官方网站或在社交媒体渠道上与我们建立联系。

现在，让我们开始今天的议程。

我们的讨论将分为两个部分：证明递归部分和ZKML部分。

我将用前半个小时来解释为什么证明递归很重要，理论的演变以及基于折叠的证明递归。

然后，Cathie博士将接过话题，介绍证明递归在实际ZKML中的应用。

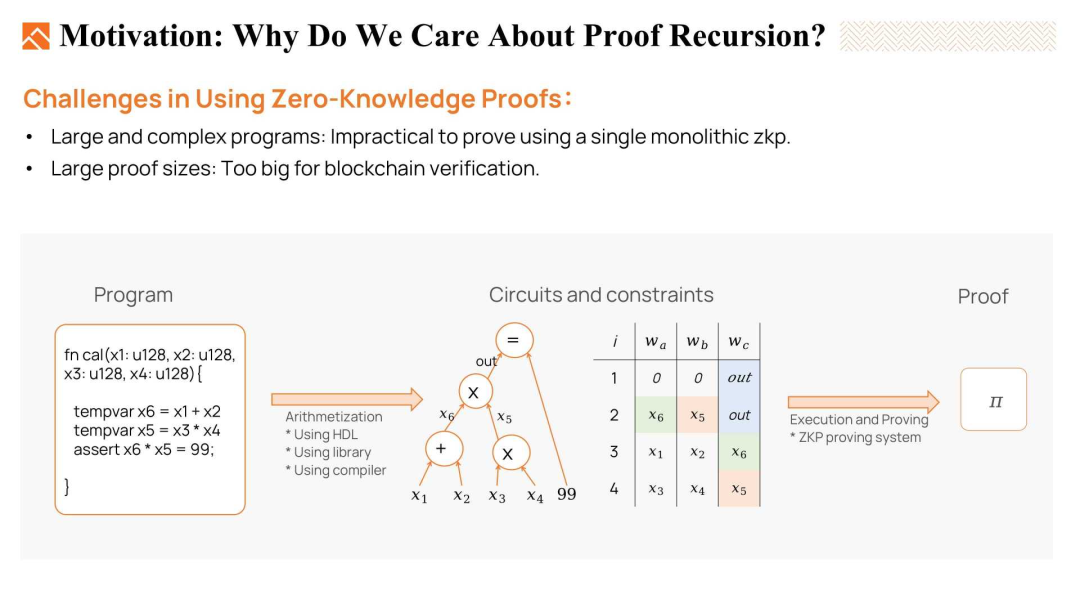
为什么我们要关注证明递归呢？

这是因为我们在使用零知识证明（ZKP）来证明程序正确执行时面临了两个挑战：

首先，将非常庞大且复杂的程序在单个整体ZKP中进行证明是低效且不切实际的。从幻灯片上的图表可以看出，我们首先需要将目标程序转换为ZKP能理解的算术电路（arithmetic circuits）或约束（constraints）。然后，我们将这些电路和见证（Witness）输入到ZKP证明系统中生成证明。之后再进行验证。包含大量计算和复杂算法的程序可能会生成庞大的电路和大量的约束。这增加了生成证明所需的计算资源。有的时候，由于证明者的内存限制，证明生成可能都无法成功执行。

此外，一些证明不适合在区块链上验证，因为区块链上有Gas限制。因此，控制证明的大小和证明验证过程的复杂性也是至关重要的。

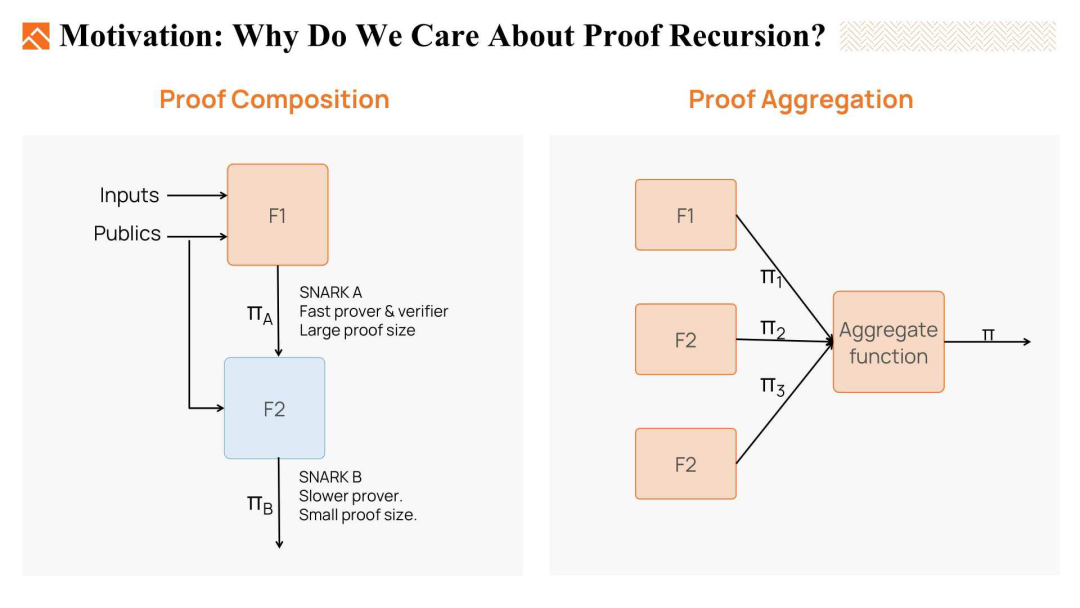为了解决这些挑战，我们通常采用三种方法：证明组合（proof composition）、证明聚合（proof aggregation）和证明递归（proof recursion）。

• 证明组合使用不同的证明系统依次生成最终证明。第一个证明系统是一个快的证明系统，但可能会生成一个较大的证明。为了减小证明的大小，我们可以运行第二个系统，该系统可能是一个较慢的证明系统，但会生成一个较短的证明。第二个证明系统将证明第一个系统的验证者会接受见证。因此，通过证明组合，我们可以构建一个快的证明系统，并且证明也较小。
• 第二种方法是证明聚合。证明聚合是将多个证明聚合成一个单一的证明。例如，zkEVM包含了许多不同的电路，如EVM电路、RAM电路、存储电路等。在实践中，验证所有这些证明在区块链上是非常昂贵的。因此，我们使用证明聚合，即使用一个证明来证明这些多个子电路证明是有效的。这个单一的证明在区块链上更容易被验证。
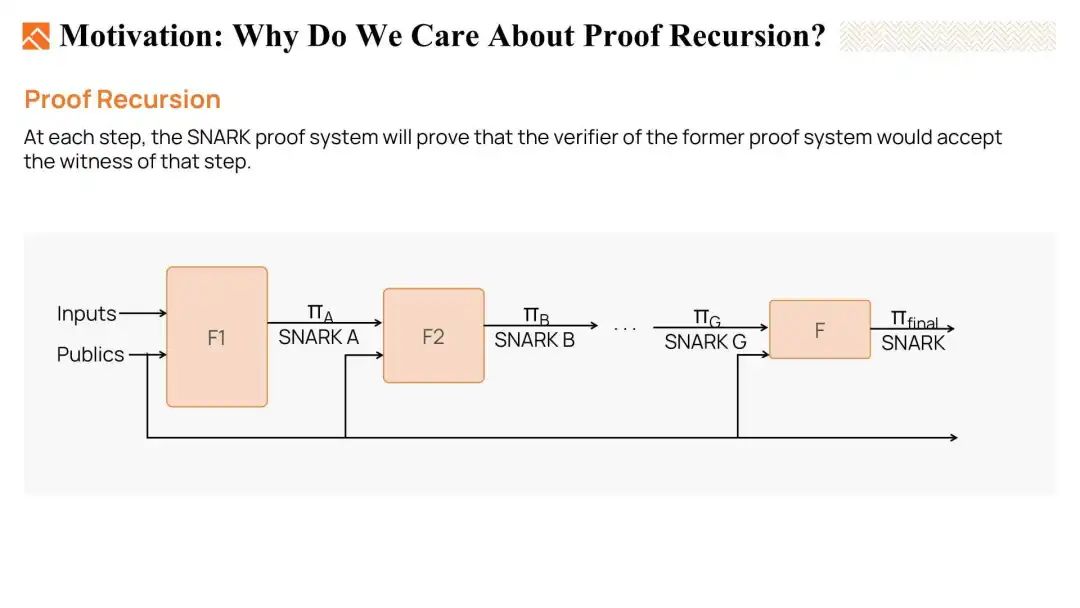• 第三种强大的方法是证明递归。证明递归的概念是构建一连串的验证者电路，在每一步中，我们可以生成一个比前一个证明更容易验证的证明。最终，我们只需要用最低的复杂度来验证最终的证明。

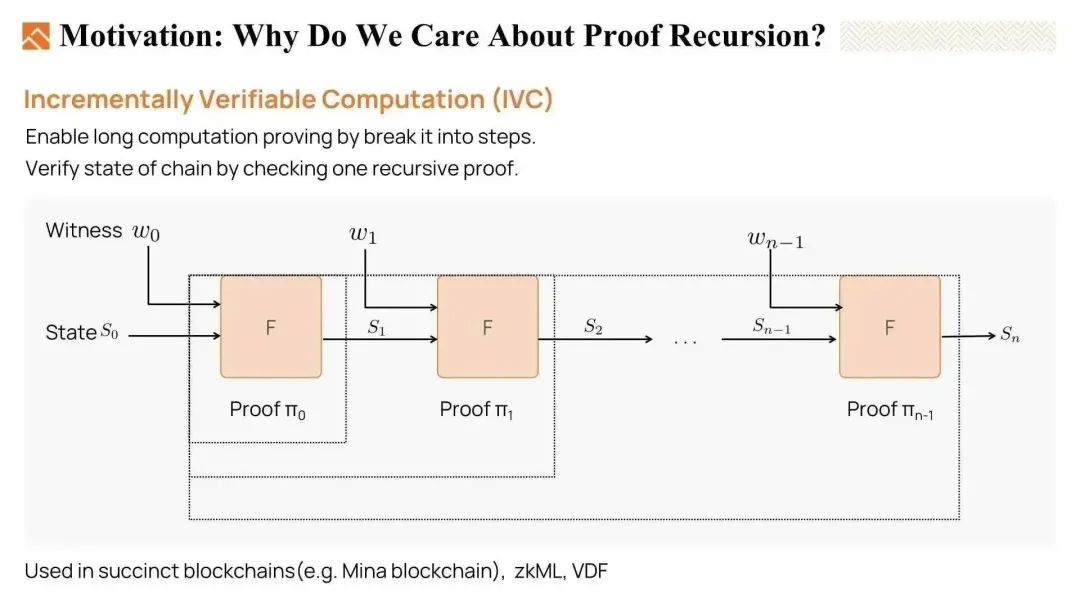证明递归可以用于实现增量可验证计算Incrementally Verifiable Computation （IVC）。

当我们有一个很长的计算，这个计算是循环执行函数F。比如，我们有一个初始状态S0，在执行F后，我们得到S1，然后重复此过程直到得到最终输出Sn。我们希望证明输出Sn是正确的结果。

证明递归在这里的作用是可以逐步更新一个证明 i 到一个证明 i +1。证明可以逐步更新，最终，我们只需验证一个证明，以确保整个执行链是有效的。

因此，它最适用于长计算和不断演化的计算。

• 对于长时间计算，我们可以将其分解为多步，并使用IVC来证明这些步骤，从而降低了证明者所需的内存大小。
• 当将这种方法应用于区块链时，它也是非常有价值的。由于区块链的状态不断增长，通过IVC证明，我们可以通过检查最新的递归证明来验证当前状态。如果该证明有效，我们可以相信整个执行历史是正确的。

总之，由于证明者的内存和时间限制，证明递归几乎是我们能够证明非常复杂的陈述的唯一方法。而且，IVC已经在简洁区块链Mina、VDF函数、ZKML等中得到了应用。

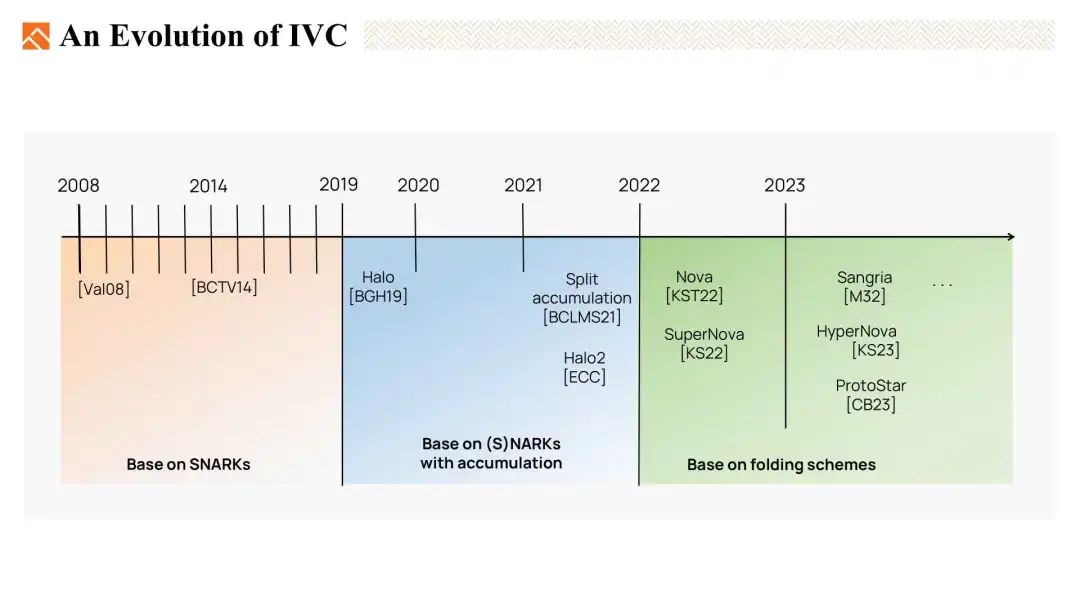
IVC技术的演变

在过去的几年中，IVC经历了三个阶段的演变。

• 第一个阶段是基于SNARKS的IVC。
• 第二个阶段基于带累加的SNARKS或NARKS的IVC。
• 最新阶段是基于折叠的IVC。这引起了当今的广泛关注。

今天，我们将简要回顾前两种类型，然后将重点放在最后一种基于折叠IVC方案上。

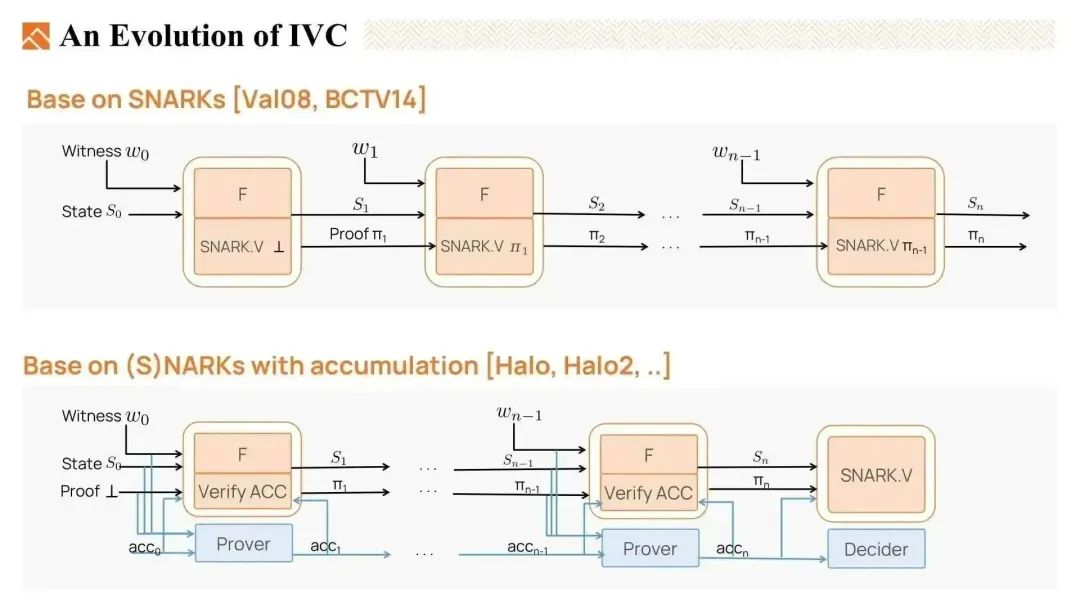• 基于SNARK的IVC原理简单。在每一步中，IVC证明者需要证明两件事情：
• 因此，IVC递归电路中嵌入了一个SNARK验证电路，并需要完全验证前一步生成的证明。这个电路庞大且昂贵。
• 函数F正确执行了，生成了状态S。
• 前一步生成的ZKP证明π是有效的。
• 第二类IVC是基于带累加的SNARKs，例如halo和halo2。它们不需要在IVC递归电路中嵌入SNARK验证电路。而是，它们引入了累加方案，将验证的昂贵部分延迟到一个累加器中，只在递归电路中保留一个小的累加验证者。累加验证者的成本远低于完整的SNARK验证者。
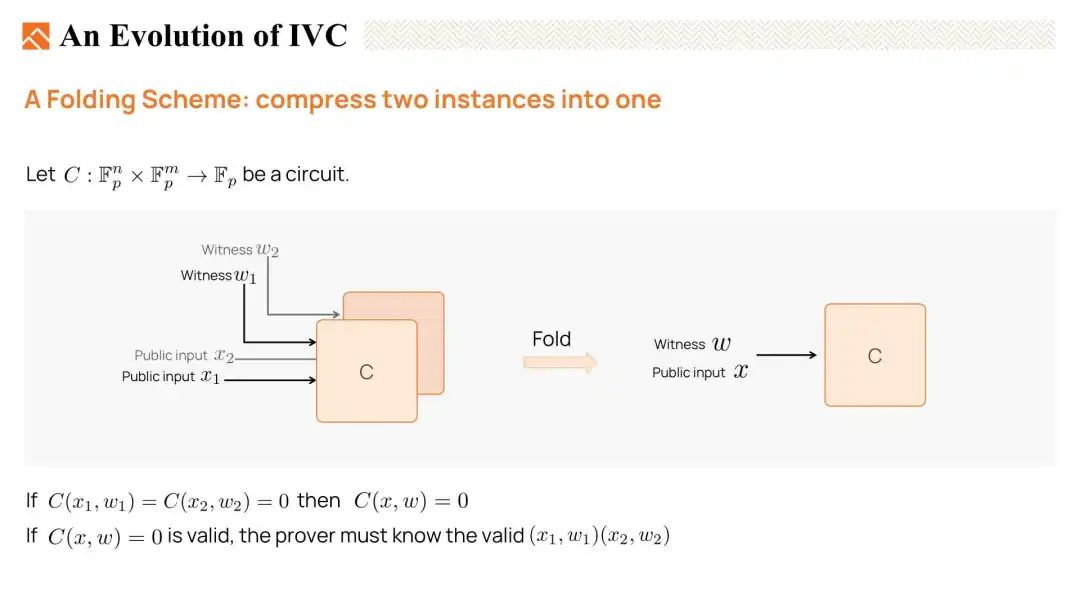• IVC 的最新阶段是基于折叠（folding schemes）的。 折叠方案最初由Nova引入。 它是一种将两个待证明的实例压缩为一个实例的方法。 假设我们有一个电路 C 和两个实例 (x1,w1) (x2,w2)。 我们想将它们折叠在一起并输出一个新的折叠实例 (x, w)。 如果两个原始实例是有效的，我们将得到一个有效的折叠实例。如果折叠实例是有效的，证明者必须知道原始实例x1和x2的有效见证w1和w2。

基于折叠的IVC技术原理

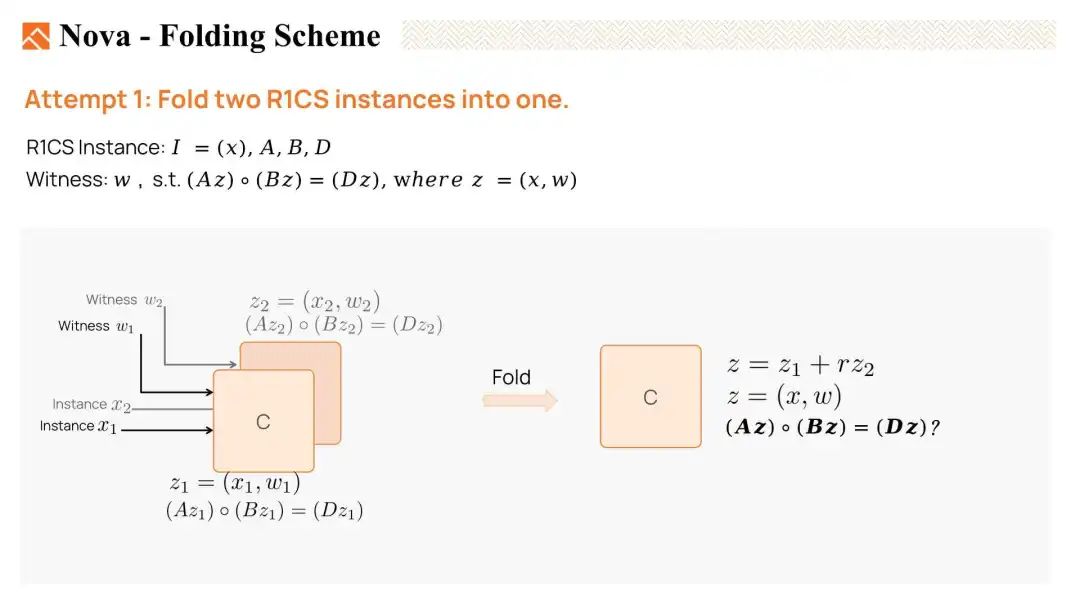
现在，让我们尝试将两个R1CS实例折叠在一起，看看是否能满足上一张幻灯片中提到的条件。

我们有两个原始见证，z1和z2（实际上是w1和w2）。z1满足方程Az1 * Bz1 = Dz1，表示它是一个有效的见证。同样，z2也是一个满足条件的见证。

然后，我们使用一个随机线性组合将它们折叠在一起，设定z = z1 + 随机数 r * z2。我们希望折叠后的见证z也是一个有效的实例。也就是说，我们希望Az * Bz = Dz。

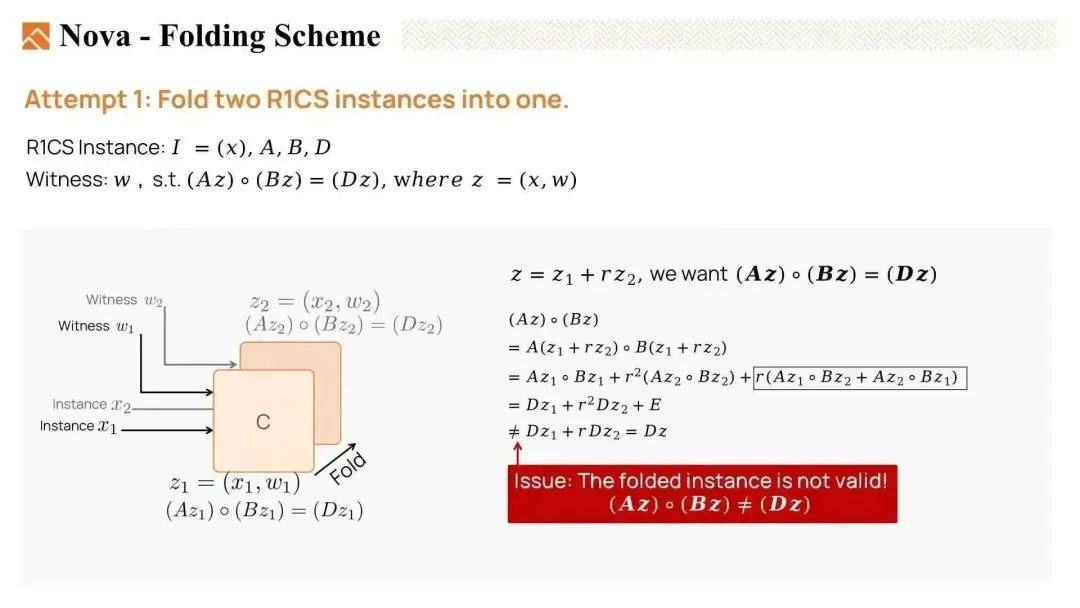但是，当我们展开Az * Bz时，会生成许多交叉项，且结果并不等于Dz。因此，z不是有效的。我们未能成功将两个R1CS实例折叠在一起。

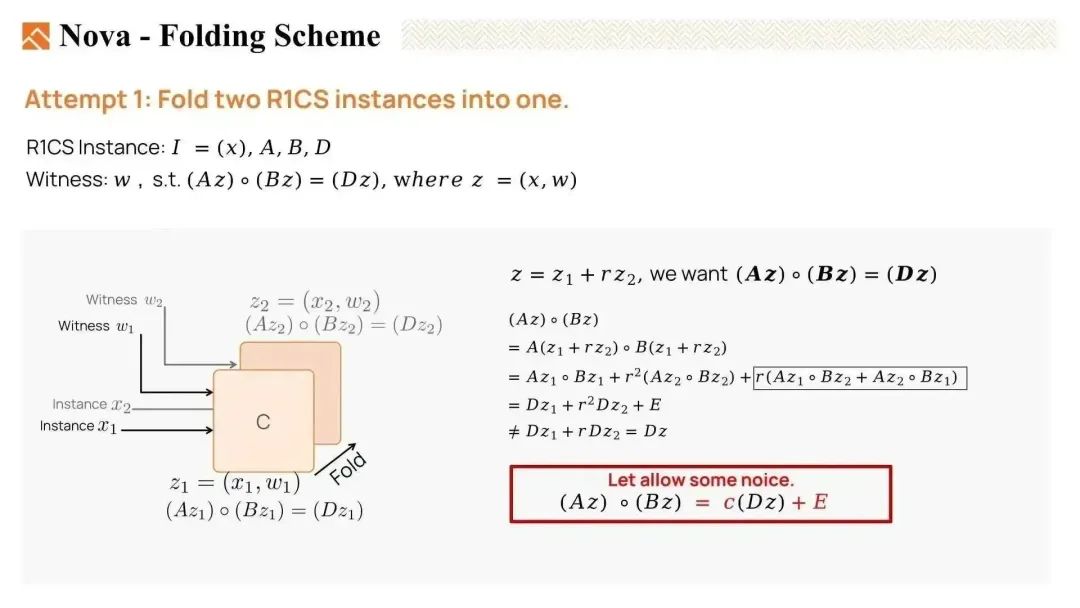然而，如果我们允许方程中存在一些噪声，它可能是相等的。Nova引入了一个误差向量（error vector）E，它吸收了折叠时生成的交叉项。还有一个标量c，用于吸收Dz的额外因子。

这个R1CS变体被称为relaxed R1CS。relaxed R1CS的实例包括x，标量c，和误差向量E。一个有效的见证z满足Az * Bz = C * Dz + E（实际上是说如果等式满足则w是有效的见证）。

我们有两个实例：*(x1, c1, E1)，其见证为w1*，和(x2, c2, E2)，其见证为w2。两个见证都是有效的。现在，让我们看看是否可以将它们一起折叠。

我们展开方程Az * Bz。最后，我们得到c * Dz + E。所以z满足了这个方程，是一个有效的见证。

现在，我们可以将z1和z2折叠在一起，得到一个新的折叠见证z，该见证对于ABD是有效的。

然而，值得注意的是，E是由E1, E2和T计算得到的，其中T包含了那些交叉项，是从见证算出来的。因此，折叠的证明者（folding prover）必须向验证者（folding verifier）提供见证以计算E。这使得折叠方案不是non-trivial的，也不是零知识的。

Not non-trivial意味着验证折叠实例可能不比验证原始的两个实例更高效，或者通信成本太大。不是零知识的，是因为在这种情况下，验证者得知了witnesses。

为了解决这个问题，我们可以用 E 和 T 的承诺(commitment)來替换 E 和 T。证明者不再向验证者发送见证，而是发送承诺以帮助验证者计算折叠的实例。

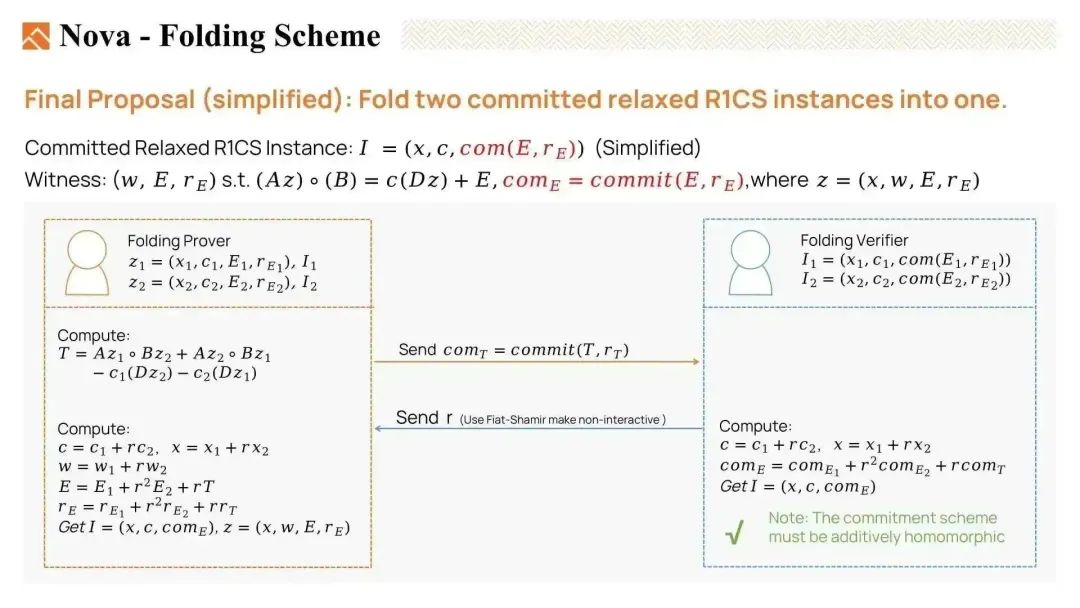因此，我们将实例中的E替换为E的承诺，并将E移动到见证中。这被称为commited relaxed R1CS。请注意，为了更容易理解，这里展示的方法是从Nova的论文简化而来的。

现在，让我们来看一下折叠方法。我们有一个折叠证明者和一个验证者。证明者有两个commited relaxed R1CS实例 I1 和 I2，以及这两个实例的见证 z1 和 z2。验证者只有实例 I1 和 I2。

• 首先，证明者将计算交叉项 T，并将 T 的承诺发送给验证者，以帮助其计算折叠实例。
• 然后，验证者选择一个随机数 r 并将其发送给证明者，我们可以使用Fiat-Shamir变换使其成为非交互式的。
• 折叠证明者计算折叠实例 I 和见证 Z。
• 验证者使用承诺 T 和原始实例 I1 和 I2，轻松计算出折叠实例 I。

如果两个原始见证 z1 和 z2 是满足条件的见证，那么折叠见证 z 将是折叠实例 I 的满足条件的见证。我们需要注意的是，承诺方案必须是加同态的。

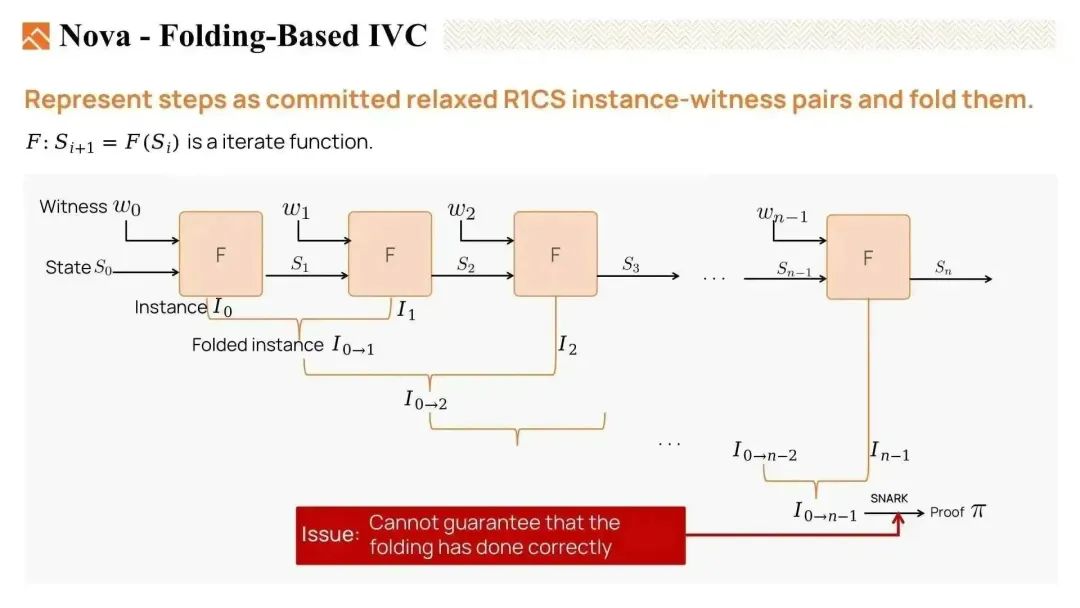在IVC中，我们可以使用折叠方案来折叠在每一步中生成的committed relaxed R1CS实例。

我们可以将实例 I0 和 I1 折叠在一起，生成一个折叠实例 I 0到1，我们也称之为运行实例。然后，将新实例 I2 与该运行实例折叠在一起，得到 I 0到2。我们重复这些步骤，得到最终实例 I 0到n-1。

最后，使用折叠后的见证，我们可以为最终的折叠实例生成ZKP证明，然后进行验证。

然而，这个证明是不完美的，因为在这里的SNARK验证者只知道折叠见证是有效的，但无法保证折叠过程是正确完成的。

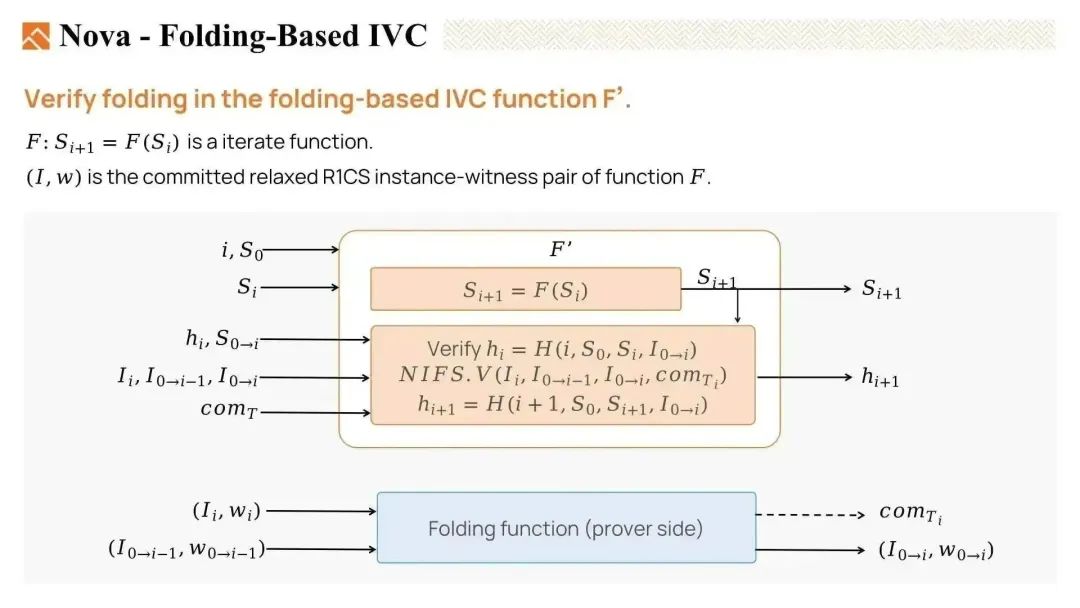因此，我们必须在每一步中验证折叠过程。

我们描述一个方法 F'，即IVC递归方法。它既包括迭代方法F，也包括能够验证折叠过程的方法。

为了验证折叠过程，我们首先验证hi，它是上一步折叠结果的哈希。然后我们验证折叠过程，即将实例 i 与运行实例 0到i-1折 叠，生成一个新实例 0到i，验证着是否正确。然后输出hi+1，即折叠结果的哈希。因此，我们通过执行一些哈希和乘法运算，以非常低的成本在每一步中验证了折叠过程。

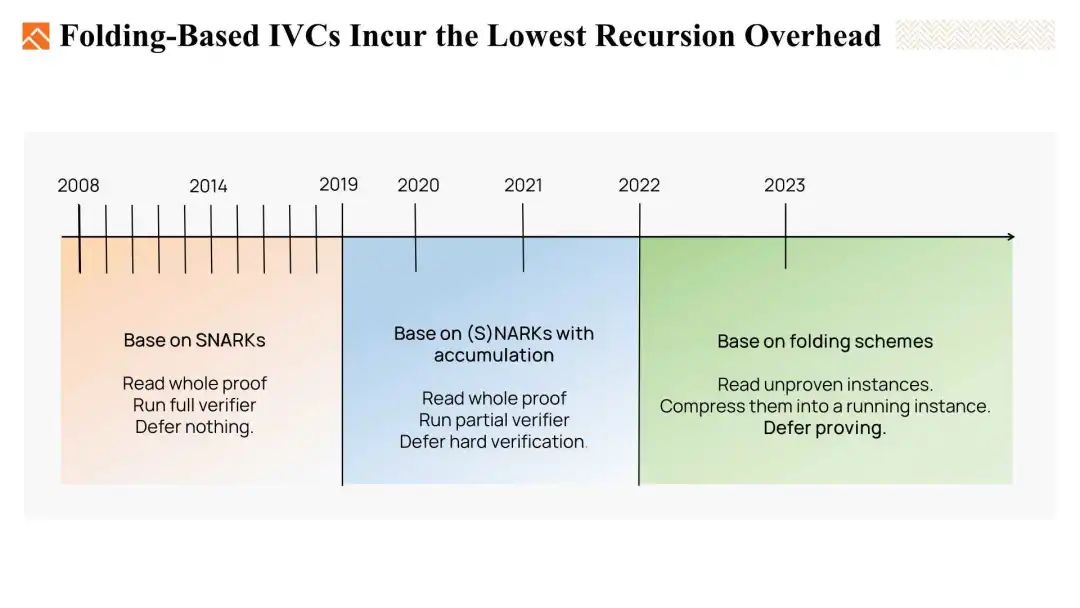总结一下，正如我们之前提到的，基于SNARK的IVC成本高昂，因为我们需要读取整个证明并在IVC递归方法中完整的验证方法。

当涉及到基于SNARK with accumulation类型的IVC时，我们仍然需要每一步都读取整个证明。但有所改进的是，我们可以将验证分为一个复杂的部分和一个简单的部分，将简单的部分在IVC链上运行，延迟复杂部分的验证。

而对于基于折叠的IVC，我们所需做的就是读取未证明的实例，并将它们折叠到一个运行实例中。折叠过程的验证很简单，就是进行一些基本的哈希和乘法运算。我们甚至可以将证明部分推迟到最后一步。与前两种方法相比，基于折叠的IVC产生的递归开销最低。因此，它们是目前最优的方法。

更多的基于折叠的IVC

在Nova的折叠方案引入后，自去年以来，我们看到了许多不同基于折叠的IVC方法。

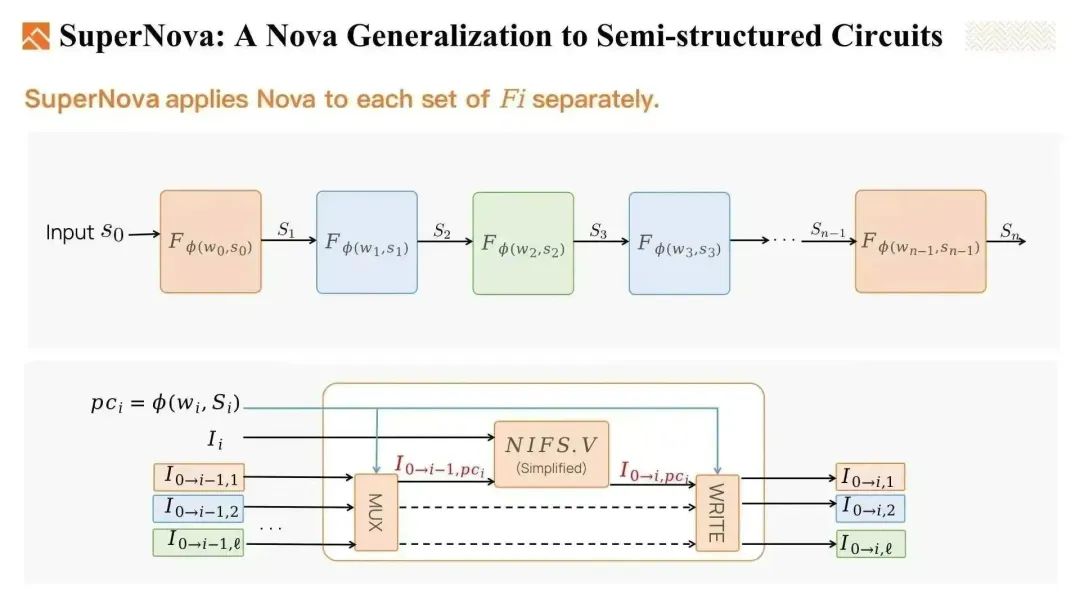
其中之一是SuperNova，它支持IVC链中存在多种方法。

给定若干非确定性方法，例如F1到F3，以及一个ϕ函数在每一步中选择其中一个F。因此，这个例子中，在IVC链中我们有3种类型的方法，而每种方法可能会出现多次。

为了折叠这些non-uniform的IVC电路实例，SuperNova将Nova应用于每组 F。使用 ϕ 函数来选出运行实例，并将当前实例折叠到运行实例中。通过这种方式，我们单独折叠每组 F。

Sangria 是 Plonk 的折叠方案，或者更准确地说，是 PLONKish 的折叠方案。

PLONKish 在定义约束和门行为方面提供了很大的灵活性。 它不仅支持加法和乘法约束(addition and multiplication constraints)，还支持复制约束(copy constraints)和自定义门约束，例如查找约束(lookup constraints)。查找约束使得 zk 不友好的方法能够被预先计算以获得更好的性能。

PLONKish功能强大，加速了各种程序的zk算数化。 Sangria 发现折叠方案可以轻松扩展到 PLONKish 约束系统。 支持加法和乘法约束、复制约束和 2 阶自定义约束。

总之，证明递归是一种非常聪明的技术，它使我们能够证明大而复杂的陈述。

基于折叠的 IVC 方案如今引起了极大的关注，并且比基于 SNARK 的 IVC 更高效。 我们相信它们将在业界得到广泛采用。

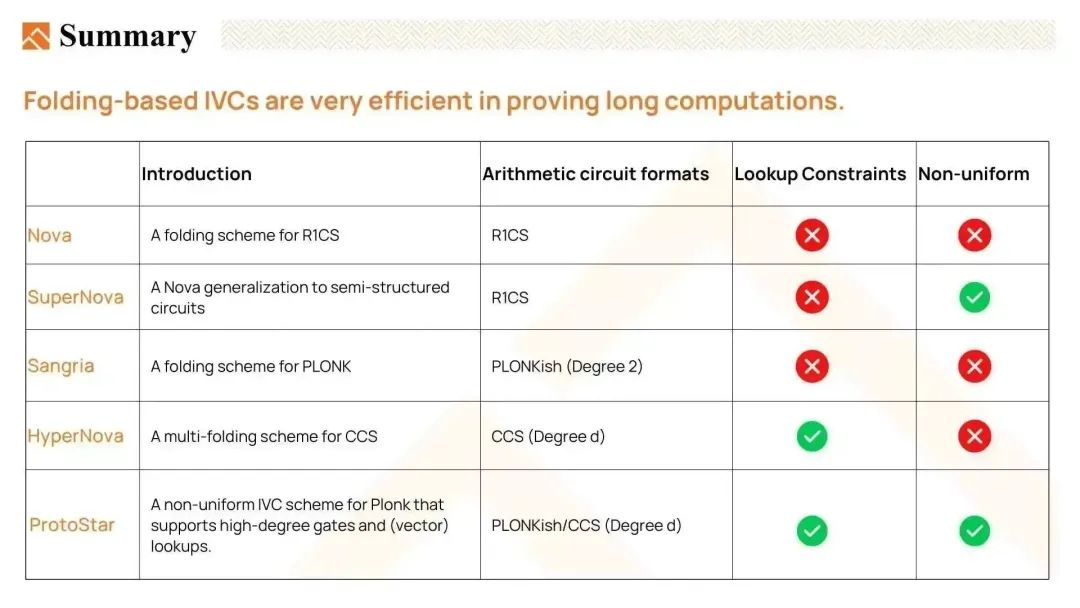
这里的图表列出了基于折叠的IVC的重要创新，让我们快速回顾一下。

• Nova，R1CS 的折叠方案，允许我们对于同一个方法的循环执行用到IVC。
• 如果我们可以在每一步执行不同的功能，那就更好了。 所以SuperNova将Nova推广到non-uniform IVC上，我们在IVC链上能运行多个方法，并且每个方法都可能在IVC上出现多次。
• Sangria 发现到 Nova 的折叠方案可以应用于 PLONKish 约束系统。 它支持复制约束（copy constraints）和2 阶的自定义约束（degree-2 custom constraints），但不支持高阶自定义约束（high degree custom constraints）和查找约束（lookup constraints）。
• HyperNova 引入了Customizable Constraint Systems（CCS）的折叠方案。 HyperNova 支持高阶自定义约束和查找约束，并使用sum-check protocol来避免执行大量的FFT（快速傅里叶变换）。
• ProtoStar 进一步增强了折叠方案，支持高阶自定义约束、查找约束和non-uniform IVC。

在结束演讲之前，我想强调，如果在座的任何人都有出色的想法，并需要资源将其付诸实践，请务必不要犹豫，随时联系我们Foresight Ventures。

此外，我们邀请您加入我们的Foresight X第二届的孵化计划。我们在这里支持并培养您的创业之路。借助我们深厚的行业知识和丰富的资源，我们将确保您的项目蓬勃发展。

此外，如果您从事学术或研究领域，Foresight X提供竞争力的Grants来支持您的研究之路。

我们在这里提供一个QR码，其中包含您可能感兴趣的所有链接，包括研究报告。请随时拍照或扫描该二维码，了解更多信息。如果演讲结束后您有任何问题，您可以在Twitter上找到我。

再次感谢您参与我们的Tech Talk。现在，我将把舞台交给Cathie博士进行下一部分的演讲。