编者注：在本系列中，我们将分享两项新的创新，它们可以显着加快 web3 中的扩展和构建应用程序：Lasso 和 Jolt。它们共同代表了一种全新的 SNARK 设计方法，可将广泛部署的工具链的性能提高一个数量级或更多；提供更好、更方便的开发者体验；并使审计变得更加容易。

有关 SNARK 为何如此重要、其当前设计状态、需要理解的关键概念以及开发人员和工程师的实现细节的更多信息，请阅读《Building on Lasso and Jolt》（其中还包括一个开源实现）。研究论文可以在这里找到（Lasso，Jolt）。您还可以在此YouTube 播放列表中观看解释 Lasso 和 Jolt、查找奇点以及思考 SNARK 设计的新方法的完整或简短视频。 

SNARK （简洁的非交互式AR知识）是一种加密协议，任何人都可以向不信任的验证者证明它知道满足某些属性的“证人” 。web3 中的一个突出应用是第 2 层 (L2) 汇总，向第 1 层 (L1) 区块链证明它们知道授权一系列交易的数字签名，因此签名本身不必由网络存储和验证。 L1，从而有助于可扩展性。 

区块链之外的应用程序包括快速但不受信任的 硬件 设备，证明它们产生的所有输出的有效性，确保用户可以信任它们。个人可以以零知识的方式证明 ，受信任的当局已向他们颁发了凭证，证明他们的年龄足以访问有年龄限制的内容，而无需透露其出生日期。任何通过网络发送加密数据的人 都可以向管理员证明该数据符合 网络策略，而无需透露更多细节。

虽然许多 SNARK 对验证者来说具有有吸引力的成本，但 SNARK 通常仍会在证明者计算中引入约六个数量级的开销。证明者所承受的额外工作是高度并行化的，但数百万倍的 因子开销严重限制了 SNARK 的应用范围。（有关更多详细信息，请参阅我之前关于 SNARK证明器性能、安全性和开发历史的帖子，以及对这种强大但复杂的技术的常见误解。） 

更具性能的 SNARK 将加速 L2，还可以允许构建者解锁尚未设想的应用程序。这就是为什么我们要引入两项新的相关技术：Lasso ，一种新的查找参数，可以显着提高证明者成本；Jolt ，它使用 Lasso 提供了一个新的框架，用于为所谓的 zkVM 和更广泛的前端设计设计 SNARK。它们共同提高了 SNARK 设计的性能、开发人员体验和可审核性，进而提高了 web3 中的构建。

我们对 Lasso 的初步实现已经证明，与流行的 SNARK 工具链 halo2 中的查找参数相比，速度提高了 10 倍以上。当 Lasso 代码库完全优化后，我们预计速度会提高约 40 倍。Jolt 包含 Lasso 之上的其他创新，我们预计它能够实现与现有 zkVM 类似或更好的加速。

查找参数、Lasso 和 Jolt 

SNARK前端是将计算机程序转换为 SNARK 后端可以摄取的电路的编译器。电路是一种极其有限的计算模型，其中可用的“原始运算”只是加法和乘法。

现代 SNARK 设计中的一个关键工具是一种称为查找参数的协议，它允许不受信任的证明者以加密方式提交一个大向量，然后证明该向量的每个条目都包含在某个预定的表中。查找参数可以通过有效地处理并非由少量加法和乘法自然计算的运算来帮助保持电路较小（请参阅我们的配套文章中讨论的按位运算示例）。

然而，正如以太坊基金会的 Barry Whitehat 去年在他称之为“查找奇点”的愿景中所概述的那样，“如果我们能够仅使用查找参数来有效地定义电路，那么它将导致更简单的工具和电路”。我们设计的电路只执行查找。正如巴里所写，随着时间的推移，查找参数“对于几乎所有事情都将变得比多项式约束更有效”。 

这一愿景与当今的工作方式形成鲜明对比，当今开发人员通过使用特殊的领域特定语言（将程序编译为多项式约束）或直接手动编码约束来编写程序来部署 SNARK。该工具链需要大量工作，并且为安全关键型错误的蔓延提供了很大的表面积。即使使用复杂的工具和电路，SNARK 的性能仍然很慢，这限制了它们的适用性。  

Lasso 和 Jolt 解决了所有三个关键问题：性能、开发人员体验和可审核性。我相信他们共同实现了查找奇点的愿景。Lasso 和 Jolt 还迫使人们重新思考 SNARK 设计中许多公认的智慧。在介绍了一些必要的背景知识后，本文重新审视了有关 SNARK 性能的一些常见观点，并解释了如何根据 Lasso 和 Jolt 等创新来更新它们。

SNARK 设计背景：为什么这么慢？

大多数 SNARK 后端都让证明者使用多项式承诺方案以加密方式承诺电路中每个门的值。然后证明者证明所提交的值确实对应于见证检查程序的正确执行。 

我将来自多项式承诺方案的证明者工作称为承诺成本。SNARK 具有来自多项式承诺方案之外的额外证明成本。但承诺成本往往是瓶颈。Lasso 和 Jolt 也是如此。如果设计一个 SNARK，其中承诺成本不是主要的证明者成本，这并不意味着多项式承诺方案很便宜。相反，这意味着其他成本高于应有的成本。 

直观上，承诺的目的是通过密码学方法安全地增加证明系统的简洁性。当证明者提交一个大的值向量时，大致就像证明者将整个向量发送给验证者，就像普通证明系统将整个见证人发送给验证者一样。承诺方案可以在不强迫验证者实际接收整个见证的情况下实现这一目标——这意味着 SNARK 设计中承诺方案的目的是控制验证者成本。

但这些加密方法对于证明者来说非常昂贵，特别是与SNARK 在多项式承诺方案之外使用的信息论 方法相比。信息论方法仅依赖于有限域运算。并且一个字段操作比提交任意字段元素所需的时间快几个数量级。 

根据使用的多项式承诺方案，计算承诺涉及多重幂运算（也称为多标量乘法，或 MSM）或FFT和 Merkle 哈希。Lasso 和 Jolt 可以使用任何多项式承诺方案，但在使用基于 MSM 的方案实例化时具有特别有吸引力的成本，例如IPA / Bulletproofs、KZG / PST、Hyrax、Dory或Zeromorph。 

为什么 Lasso 和 Jolt 很重要

Lasso 是一种新的查找参数，其中证明者承诺比以前的工作更少且更小的值。根据上下文，这可能会导致 20 倍或更多的加速，其中 2 到 4 倍的加速来自于较少的提交值，另一个 10 倍的加速来自于 Lasso 中所有提交的值都很小的事实。与许多先前的查找参数不同，Lasso（和 Jolt）还避免了FFT ，FFT 占用大量空间，并且可能成为大型实例的瓶颈。 

此外，Lasso 甚至适用于巨大的表（比如大小为 2 128），只要这些表是“结构化的”（在精确的技术意义上）。这些表太大，任何人都无法显式实现，但 Lasso 只为其实际访问的表元素付费。特别是——与之前的查找参数相比——如果表是结构化的，那么任何一方都不需要以加密方式提交表中的所有值。

Lasso 利用两种不同的结构概念：可分解性和LDE 结构。 （LDE 是称为低次扩展多项式的技术概念的缩写。） 可分解性大致意味着可以通过对更小的表执行少量查找来回答对表的单次查找。这是比 LDE 结构更严格的要求，但 Lasso 在应用于可分解表时特别有效。  

Jolt

Jolt（Just One Lookup Table ）是一种新的前端，由 Lasso 使用巨大的查找表的能力解锁。Jolt 的目标是虚拟机/CPU 抽象，也称为 指令集架构(ISA) 。支持这种抽象的 SNARK 称为 zkVM。例如，考虑RISC-Zero 项目也针对的RISC-V 指令集（包括乘法扩展）。这是由计算机体系结构社区开发的一种流行的开源 ISA，没有考虑到 SNARK。 

对于每个 RISC-V 指令fi ，Jolt 的主要思想是创建一个包含fi的整个评估表的查找表。因此，如果fi采用两个 32 位输入，则该表将有 2 64 个条目，其中 ( x , y )的第一个条目是fi ( x , y )。如果我们考虑 64 位而不是 32 位数据类型的指令，则每条指令的表的大小将是 2 128而不是 2 64。 

对于基本上每个 RISC-V 指令，生成的查找表都是可分解的，并且套索适用。（少数指令是通过应用一小段其他指令来处理的。例如， 除法 是通过让证明者提交商和余数来处理的，并通过一次乘法和一次加法检查这些是否正确提供。）

然后可以生成运行 RISC-V CPU T个步骤的“电路”，如下所示。对于T个步骤中的每一个，电路都包含一些简单的逻辑，用于确定该步骤要执行的原始 RISC-V 指令f i是什么，以及该指令的输入 ( x , y )是什么。然后，电路 简单地通过执行查找来执行f i ，该查找显示关联表的第( x , y ) 个条目。更准确地说，Jolt 考虑由每条指令的表串联组成的单个表 - 因此称为“仅一个查找表”。 

重新审视 SNARK 设计中公认的智慧

Lasso 和 Jolt 还颠覆了 SNARK 设计中的一些公认的智慧。每条公认的智慧都以粗体字显示，后面是 Lasso 和 Jolt 如何改变事物。

#1. 大面积的 SNARK是一种浪费。每个人都应该使用FRI、Ligero、Brakedown或变体，因为它们避免了通常适用于大范围的椭圆曲线技术。

这里的字段大小大致对应于 SNARK 证明中出现的数字的大小。由于非常大的数字的加法和乘法成本很高，因此大字段上的 SNARK 是浪费的想法意味着我们应该努力设计永远不会出现大数字的协议。基于 MSM 的承诺（定义如下）使用椭圆曲线，椭圆曲线通常是在大字段（大小约为 2 256）上定义的，因此这些承诺因性能较差而闻名。 

我之前的文章解释说，使用小字段是否有意义（即使它们是一个选项）在很大程度上取决于应用程序。Lasso 和 Jolt 走得更远。他们表明，即使使用基于 MSM 的承诺方案，证明者的工作也几乎可以独立于字段大小。这是因为，对于基于 MSM 的承诺，承诺值的大小比这些值所在字段的大小更重要。

有关 MSM 的详细信息。大小为n的多次幂运算 （也称为 MSM）计算以下形式的表达式

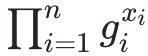
，其中每个gi是乘法群的元素。朴素多重求幂算法执行n组求幂和n组乘法。每次求幂可能比乘法慢约 400 倍。

Pippenger 的多重求幂算法比朴素算法节省了大约 log( n )的因子。实际上，这可能远远超过 10 倍。此外，如果所有指数都很“小”（例如，在 0 和 2^20之间），则可以在多次取幂时间中节省 10 倍的因子。这类似于计算

比计算

速度快 10 倍。前者涉及16次平方，后者涉及160次。 

如果所有提交的值都很小，Pippenger 的算法只需要（大约）一组乘法 来提交一个值（请参阅本文第 4 节以获得很好的说明）。

Lasso 和 Jolt 的新属性。现有的 SNARK 使证明者承诺许多随机 字段元素。例如，名为Plonk的流行 SNARK 后端中的证明者承诺每个电路门大约 7 个随机场元素（以及其他非随机场元素）。即使被证明的计算中出现的所有值都很小，这些随机场元素也会很大。 

相比之下，Lasso 和 Jolt 仅要求证明者提交较小的值（Lasso 的证明者提交的值也比先前的查找参数少）。这极大地提高了基于 MSM 的方案的性能。至少，Lasso 和 Jolt 应该废除这样的观念：在证明者性能很重要的情况下，社区应该放弃基于 MSM 的承诺。

#2：更简单的指令集带来更快的 zkVM。 

只要每条指令的评估表是可分解的，Jolt 的（每条指令）复杂度仅取决于指令的输入大小。Jolt 证实，令人惊讶的复杂指令是可分解的，特别是所有 RISC-V。

这与人们普遍认为的观点相反，即更简单的虚拟机 (zkVM) 必然会导致更小的电路和相关的更快的证明器（VM 的每一步）。这是特别简单的 zkVM（例如Cairo VM）背后的指导动机，它们是专门为 SNARK 友好而设计的。 

事实上，对于更简单的虚拟机，Jolt 为证明者实现了比之前的 SNARK 更低的承诺成本。例如，对于 Cairo VM 执行，SNARK 证明者在 VM 的每个步骤中提交 51 个字段元素。Cairo 部署的 SNARK 当前在251 位字段上工作（63 位是 SNARK 可以使用的字段大小的硬下限）。Jolt 的证明器致力于 RISC-V CPU 的每步约 60 个字段元素（定义超过 64 位数据类型）。考虑到提交的字段元素很小的事实后，Jolt 证明者的成本大致相当于提交 6 个随机 256 位字段元素的成本。

＃3：将大型计算分解为小块不会造成性能损失。 

基于这种观点，当今的项目将任何大电路分解成小块，分别证明每个块，并通过 SNARK 递归聚合结果。这些部署使用这种方法来缓解流行 SNARK 中的性能瓶颈。例如，基于 FRI 的 SNARK 需要接近 100 GB 的证明空间，即使对于小型电路也是如此。它们还需要 FFT，这是一种超线性运算，如果 SNARK“同时”应用于大型电路，则可能成为瓶颈。

现实情况是，一些 SNARK（例如 Lasso 和 Jolt）表现出规模经济（而不是当前部署的 SNARK 中的规模不经济）。这 意味着被证明的语句越大，相对于直接证人检查（即在不保证正确性的情况下评估证人电路所需的工作），证明者开销越小。在技​​术层面，规模经济来自两个地方。 

1. n大小的 MSM的 Pippenger 加速：相对于朴素算法的log( n ) 因子改进。n越大，改善越大。
2. 在 Lasso 等查找参数中，证明者支付“一次性”成本，该成本取决于查找表的大小，但与查找的值的数量无关。一次性证明者成本在对表的所有查找中进行摊销。更大的块意味着更多的查找，这意味着更好的摊销。

当今处理大型电路的流行方法是将事物分解成尽可能小的部分。每个部分的大小的主要限制是它们不能太小，以至于递归聚合证明成为证明者的瓶颈。 

Lasso 和 Jolt 提出了一种本质上相反的方法。人们应该使用具有规模经济性的 SNARK。然后将大型计算分解为尽可能大的部分，并对结果进行递归。每个片段大小的主要限制是证明空间，它随着片段变大而增长。

#4：高度约束对于高效的 SNARK 是必要的。 

Jolt 使用 R1CS 作为其中间表示。在 Jolt 中使用“高度”或“自定义”约束没有任何好处。Jolt 中的证明者成本大部分在于查找参数 Lasso，而不是证明将查找视为理所当然的结果约束系统的可满足性。 

Jolt 是通用的，因此它不会失去通用性。因此，它反驳了开发人员对设计高度约束（通常是手动指定）的强烈关注，以努力从当今流行的 SNARK 中挤出改进的性能。 

当然，某些上下文仍然可能受益于高度或自定义约束。一个重要的例子是Minroot VDF，其 5 度约束可以将承诺成本降低约 3 倍。

＃5：稀疏多项式承诺方案成本高昂，应尽可能避免。

这是针对最近引入的名为CCS 的约束系统和支持它的 SNARK 的主要批评——（超级）斯巴达和（超级）马林鱼。正如我在上一篇文章中所讨论的，CCS 是当今实践中流行的所有约束系统的清晰概括。 

这种批评是没有根据的。事实上，Lasso 和 Jolt 的技术核心是Spartan中的稀疏多项式承诺方案（参见第 7 节），称为 Spark。Spark 本身是将任何（非稀疏）多项式承诺方案通用转换为支持稀疏多项式的方案。 

Lasso 优化并扩展了 Spark，以确保证明者只承诺“小”值，但即使没有这些优化，批评也是不合理的。事实上，Spartan 的证明者比SNARK （例如避免稀疏多项式承诺的 Plonk）承诺更少的（随机）字段元素。

正如我在上一篇文章中所讨论的，Spartan 的方法具有额外的性能优势，特别是对于具有重复结构的电路。对于这些电路，加法门不会增加 Spartan 证明者的加密工作。这项工作仅随着给定约束系统中变量的数量而增长，而不是随着约束的数量而增长。与 Plonk 不同的是，Spartan 证明者无需提交同一变量的多个不同“副本”。

***

我们乐观地认为 Lasso 和 Jolt 将极大地改变 SNARK 的设计方式，从而提高性能和可审计性。本系列的后续文章将更深入地探讨 Lasso 和 Jolt 的工作原理。特别是，我将解释他们对和检查协议的使用，这是一种具有神奇能力的关键工具，可以最大限度地减少证明者的承诺成本。随着我们继续优化 Lasso 和构建 Jolt，我们欢迎来自社区的反馈。您可以在这里联系我，我也会在那里宣布未来的工作。 

***

致谢：Justin Thaler 与同事Srinath Setty（微软研究院）、Riad Wahby（卡内基梅隆大学）和Arasu Arun（纽约大学）一起开发了 Lasso 和 Jolt；Lasso 的实现是由 a16z 加密工程师Sam Ragsdale和Michael Zhu完成的。 

***

Justin Thaler是 a16z 的研究合伙人，也是乔治城大学计算机科学系的副教授。他的研究兴趣包括可验证计算、复杂性理论和海量数据集算法。