前段时间在翻译一本零知识证明技术的书。上个月底基本内容已经翻译完成。翻译时间比我预想的长得多。目前正在和作者讨论书中的一些笔误，准备最后的定稿。

anyway，终于有点时间看看新鲜东西。先从Nova算法开始～

01

Nova算法相关资料

三份资料可以帮助理解Nova算法：

1. Nova论文：https://eprint.iacr.org/2021/370.pdf
2. Nova潜在攻击和相应修正：https://eprint.iacr.org/2023/969.pdf
3. Nova潜在攻击的理解总结：https://www.zksecurity.xyz/blog/posts/nova-attack/

本文是上述资料的理解和总结。本文中的一些图来自于上述资料，在本文中不再一一标注。

02

从IVC开始

Nova算法是一种针对IVC（增量可验证计算，Incrementally Verifiable Computation）的新型的零知识证明算法。IVC，即同一个函数把前一个输出作为下一个输入迭代计算。F函数的迭代计算过程如下图：

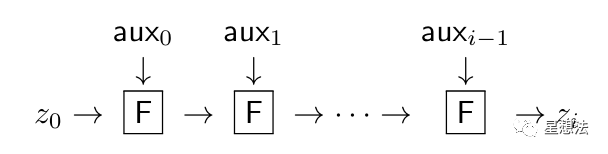
z0是最初的输入，通过F函数计算生成的结果，作为下一个F函数的输入。

03

松弛R1CS以及松弛承诺R1CS

众所周知，R1CS是零知识证明技术中电路约束表示形式。松弛R1CS（Relaxed R1CS)可以看成是R1CS的扩展形式。在R1CS的基础上，增加一个标量u以及一个错误向量E。松弛R1CS的实例用(E, u, x)表示。

松弛承诺R1CS在松弛R1CS的基础上，将E以及W向量承诺。松弛承诺R1CS的实例用（\bar{E}, u, \bar{W}, x)表示，其中x和u是公开变量。

从R1CS扩展到松弛R1CS，是为了折叠方案。注意的是，从松弛R1CS的角度看，R1CS是其的一种特例。也就是说，R1CS也是一种“特别“的松弛R1CS。

04

折叠方案（Folding Scheme）

直觉上来说，一个关系R的折叠方案就是将两个符合关系R的实例“折叠成”一个新的复合关系R的实例。松弛R1CS/松弛承诺R1CS就能进行类似的折叠。两者的折叠过程类似。松弛承诺R1CS的折叠方案如下：

整个折叠方案由4步组成。第一步，证明者P发送一个交叉项T的承诺\bar{T}给验证者。第二步，验证者发送随机挑战r给证明者。第三步是证明者和验证者都需要执行的，承诺的折叠。第四步，证明者独自执行，将两个实例的E和W向量进行折叠。

05

增广函数F' （Argumented Function)

折叠方案，折叠的是松弛R1CS实例。那这些松弛R1CS实例证明的计算是什么？显然，这些计算要包括折叠的计算。这些计算不仅仅是IVC计算中的F函数了，也就被称为增广函数F‘。增广函数F’的计算主要由两部分组成：

1/ IVC中的F函数

2/ R1CS实例的折叠计算

06

理想中的样子

有了上述的这些理解，可以想象出折叠的过程：

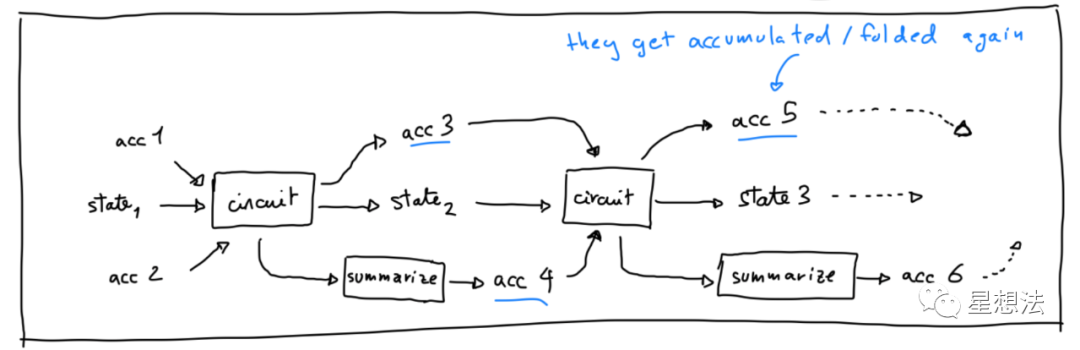
其中，circuit就是增广函数F’对应的电路。acc{1,2,3,4,5,6}是松弛承诺R1CS实例。circuit有两个计算：1/松弛承诺R1CS实例的折叠，比如acc1+acc2->acc3。2/计算F函数，将状态state1变为state2，再从state2变为state3等等。

注意的是，增广函数F’对应的circuit，本身也是一个R1CS实例，其可以表示成松弛R1CS实例。也就是图中的acc4和acc6。“summarize”是将松弛R1CS实例转换为松弛承诺R1CS实例。

仔细观察第二个电路的输入，acc3是折叠后的松弛承诺R1CS实例，acc4是证明acc3是正确折叠结果的松弛承诺R1CS实例。这两个实例会进入下一次的折叠，生成acc5。你可以试想一下，如果acc3以及acc4是可满足的松弛承诺R1CS实例，意味着，acc3是由两个可满足的松弛承诺R1CS实例折叠而来，也就是说，acc1以及acc2是可满足的松弛承诺R1CS实例。这样的可靠性也就可以一步步“向”前推导，从而也证明了每一次circuit中的F函数计算是正确的。总的来说，就是通过某一个circuit对应的两个松弛承诺R1CS实例的可满足性，可以证明之前所有的IVC计算是正确的。

07

真实的样子

熟悉零知识证明的朋友，都知道多项式承诺方案中经常采用椭圆曲线。scalar域上对应的多项式的承诺是用椭圆曲线的base域表示。R1CS电路通常是采用scalar域来表示。仔细看，上图中的“summarize”的前后涉及到域的转换。也就是，要将circuit对应的松弛承诺R1CS实例进行折叠的话，必须在另外一个电路中去“折叠”。这时，需要引入椭圆曲线循环，两个或者多个椭圆曲线，其中一个曲线的scalar域，和另外一个曲线的base域相同，巧的是，该曲线的scalar域和之前曲线的base域相同。采用这样的椭圆曲线循环，可以将“理想中的样子”实现：

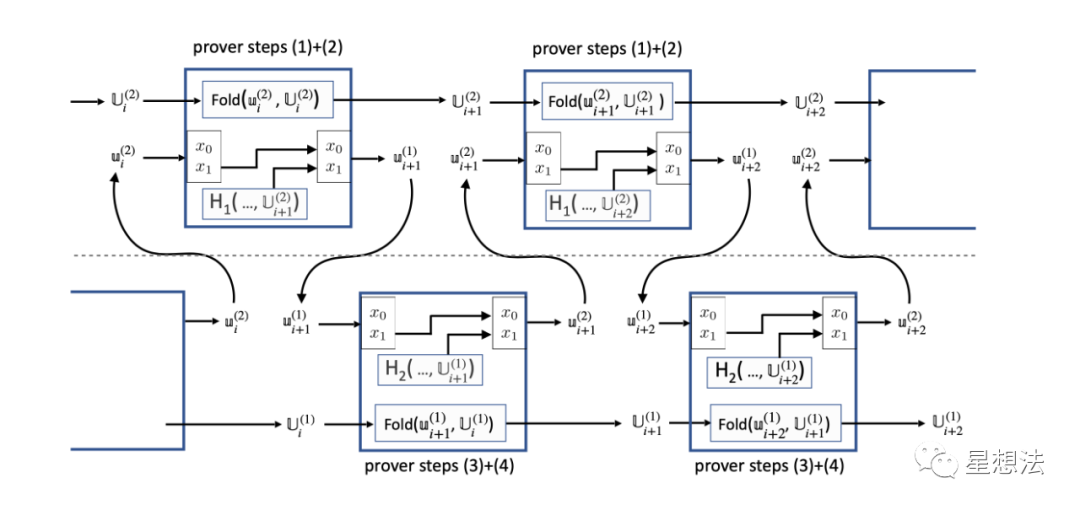
整个折叠过程，拆分成两个电路进行折叠。上部分可以称为Circuit 1的折叠，下部分可以称为Circuit 2的折叠。两个电路的关系的形式化表示在论文“Nova潜在攻击和相应修正”的第8页。U表示的是折叠后的实例，u表示的是一个R1CS实例对应的松弛实例。注意的是，Circuit 1折叠的是Circuit 2对应的松弛承诺R1CS实例，而Circuit 2折叠的才是Circuit 1对应的松弛承诺R1CS实例。Circuit 2的主要目的就是折叠Circuit1对应的松弛承诺R1CS实例，其电路中的函数计算没有意义。相反，F函数实现在Circuit 1中。结合“理想中的样子”，大致可以猜到U{i+2}^2, u{i+2}^1, u{i+2}^2, U{i+2}^1可满足性是证明的重要部分。

因为“电路”切割成两部分，并且各自的电路在另外的电路中进行折叠。存在几个实例之间的绑定问题：u和U实例之间的绑定以及u实例在两个电路之间传递的绑定。为了解决这些绑定问题，在电路中引入了x_0/x_1公开变量，其中x_1指定了和u实例绑定的电路输出U实例和当前的F函数的输出（为了简化电路结构，在图中未体现）。你想，在电路中引入了U实例的H_1结果的话，如果u实例是可满足的，x_0/x_1既是真实可靠的，即和U进行了“绑定”。x_0建立的是输入的u和U的绑定关系，x_1建立的是输出的u和U的绑定关系。

举个例子，u{i+1}^1作为下半部分电路的输入时，经过Circuit 2，其输出u{i+1}^2.x0 = u{i+1}^1.x1，这样，再输入到上半部分电路时，如果u{i+1}^2可满足的话，则其的x_0应该等于U_{i+1}^2的H1的结果。这在Circuit 1电路中会进行检查。这样，就保证了正确的实例，在两个电路之间传递。

08

IVC的证明

为了证明IVC在某个迭代正确计算，逻辑上需要证明如下信息：

除了证明四个实例可满足外，还需要证明两个x1的绑定关系，示意如下图：

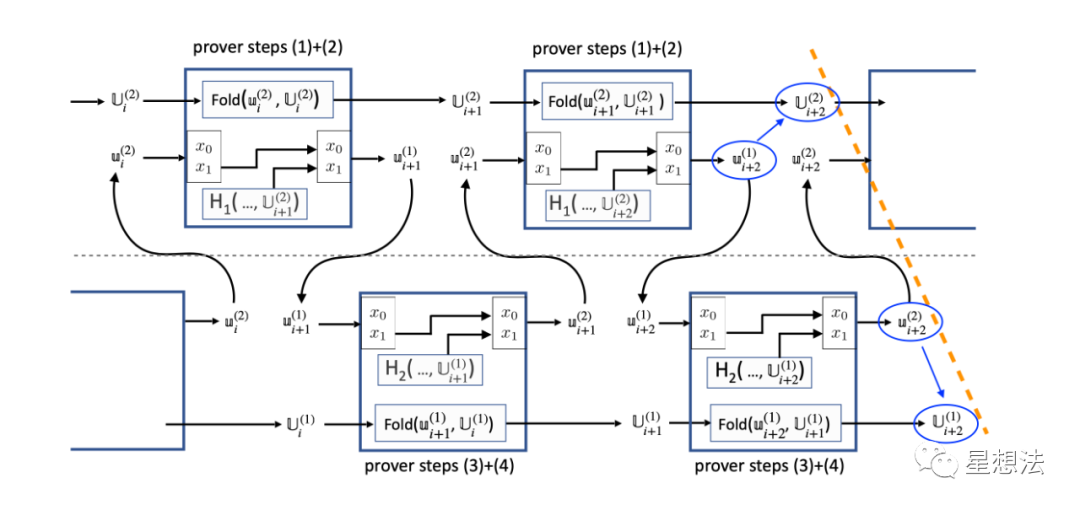
这些信息是否正确，需要额外的证明电路实现。也就是说，IVC计算的证明是该电路的证明。可想而知，如果是很多次迭代的计算，原本需要将这些迭代一个个地在电路中展开，现在只需要对4个电路实例进行可满足性以及绑定关系的验证即可。性能提升非常大。

09

攻击以及算法修正

看到上面的图，有个直觉，怎么感觉上下电路的实例是“割裂“的，没有什么绑定性。事实上，攻击就是这样构造的。

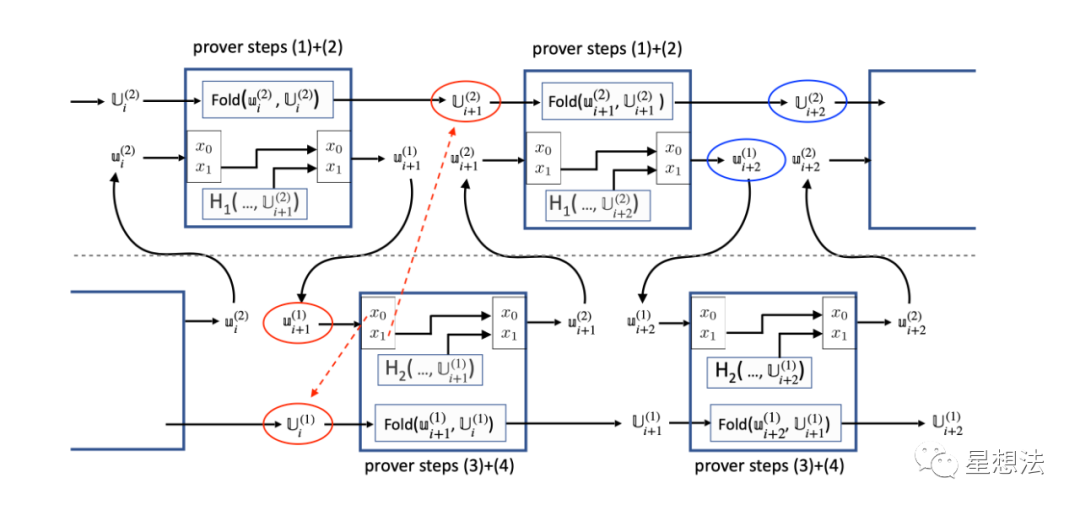
伪造U_i^1和U{i+1}^2，虽然是伪造的，但是是可满足的实例。伪造u{i+1}^1，修改x_0和x_1和伪造的U实例对应。显然，u{i+1}^1实例不满足。虽然它不满足，但是Circuit 2的电路还是可以满足的，只是输出U{i+1}^1实例不满足而已。成功构造了u{i+1}^2的话，Circuit 1就可以构造出可满足的u{i+2}^1以及U_{i+2}^2，并且满足x1的绑定关系。这样就先构造出了最终伪造证明的一半内容。通过对称性，可以构造出下面一半的输出实例。通过两次构造的结果的“拼接”，可以伪造出IVC计算的证明。

修正后的检查逻辑如下：

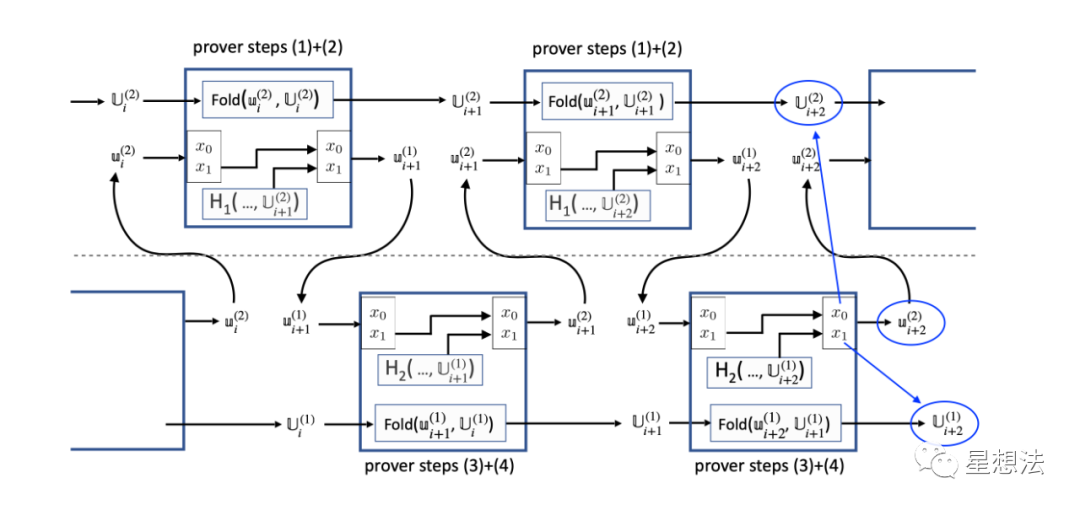
“Nova潜在攻击和相应修正”论文的第6章给出了详细的安全性分析。感兴趣的小伙伴，可以自行查看原论文。

Nova的基本思想是通过折叠方案折叠电路实例。逻辑比较绕，需要仔细地思考电路折叠过程以及实现电路中的绑定关系。

一个字形容：绝～