“我们采用既定的TradFi衍生品定价理论来得出AMM自动化做市策略。 本文探讨了该技术的历史根源，并展示了我们如何将其应用于做市。 通过由此产生的定价机制，如果AMM保持平衡，交易者将面临较低的滑点。 如果AMM面临风险，滑点就会增加，并激励交易者对冲AMM净风险敞口。”

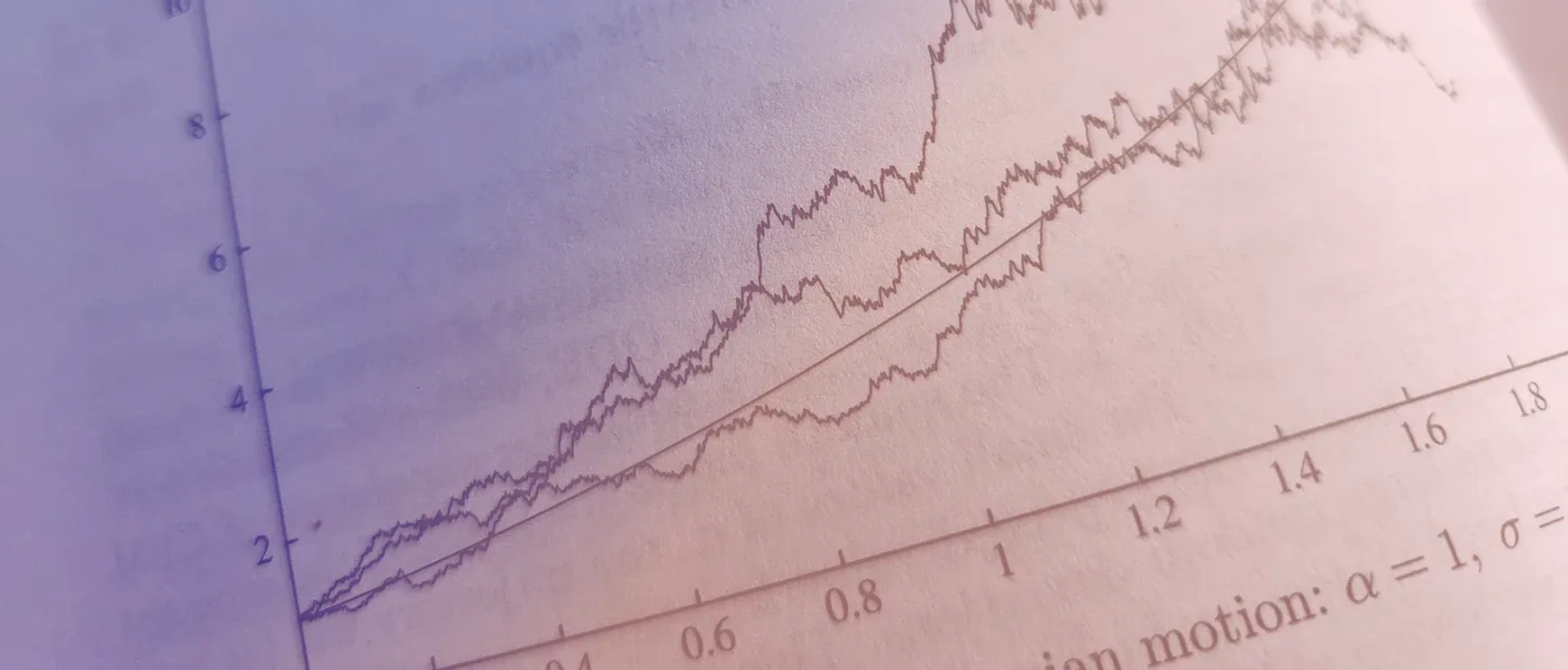
Merton的债券定价模型（Merton，1974）假设公司有一定数量的到期日为T的债务。如果公司的资产价值在T时低于债务的面值，公司就会违约。在这个模型中，公司的权益是公司资产的欧式看涨期权，其行权价格等于债务的面值。这个模型可以用来预估公司的违约概率，正如Moody’s公司所商业化的KMV Merton模型[Bharat, Shumway, 2008]，也可以用来定价公司的信用风险债务[Moody’s, 2022]。

继Merton在1974年发表的文献后，出现了其他的违约风险模型。在[Black, Cox, 1976]模型中，公司也可以在到期日T之前违约，而在Merton的方法中固定的违约阈值现在是动态的。特别是在90年代末信用衍生品的兴起，抽象出公司资产负债表的模型（称为简化模型），开始受到关注。关于结构模型和简化模型的详细内容，请参见附录A。

结构模型和简化模型这两种方法，都是模拟违约风险和定价信用的有效方法。这两种模型都可以从历史数据进行校准，有时它们被结合成“混合”形式。当这些模型用于定价时，它们共同遵循的是风险中性估值原则。

风险中性估值

简而言之，这一原则表明，资产的价值等于期望的、贴现的现金流的价值。期望值不是使用真实世界的概率来计算的，而是使用从其他资产价格中提取出来的构造概率来计算的。关于这种估值方法还有很多内容可以展开，但就本文章而言，重点是知道这是衍生品的定价方法，如欧式看涨和看跌期权、CDS或结构化产品。对于我们与D8X合作的定量分析师来说，[Björk, 2009]是风险中性估值的一个较好的参考。

永续AMM面临市场风险

自动化做市商（AMMs）是订单簿市场的DeFi替代品。AMMs使用公式确定给定交易的价格，而不是在基于订单簿的系统中匹配限价和市价订单。

假设只有一个交易员在永续合约中做多1 ETH（例如参见[Deribit 2022]对永续合约的解释）。如果ETH的价格上涨20%，AMM欠交易员收益部分的金额。同样，如果价格下跌20%，AMM会减少交易员的保证金，以亏损的金额为准。简而言之，AMM面临市场风险。

如果有另一个交易员做空1 ETH，价格上涨20%，做空的交易员损失了20%，做多的交易员获得了20%，反之亦然，如果价格下跌20%。在这个例子中，AMM的市场风险抵消为零：无论价格如何变动，AMM都不会产生任何损失或收益。

总之，对于AMM来说，最好是净零敞口。严格地说，“零”只适用于线性永续合约。在本文中，我们关注的是线性永续合约，其中抵押品以持有的报价货币（例如，对于ETH-USDC永续合约，抵押品为USDC）。

AMM作为保险提供者

为了确定D8X永续合约的价格，我们假设交易员以现货价格进入合约，如果他们增加了AMM的敞口，他们还会从AMM购买信用保险。信用保险旨在保证当交易员关闭头寸时，按照合约规定支付给交易员应得的金额。如果交易员减少了AMM的敞口，他们将会获得退款。如果AMM在交易员想要结算时没有资金，应付的金额需要从违约基金（即额外的资本储备）中支付。因此，与AMM的交易还包括可能进入保险基金。根据AMM的状态，保险费用更高，或者，正如我们将看到的，如果他们减少了AMM的敞口，交易员会得到退还的保险费。

深入探讨：永续期货AMM的结构模型

我们如何定价这种信用保险呢？类似于Merton的债券定价模型，我们假设一个固定的时间范围T。为了解释这个概念，我们首先假设AMM只有一个交易员和一个以报价货币（例如USDC）表示的资本M。交易员在指数价格s处进入一个（signed）大小为κ的头寸。固定时间段结束时的交易员利润为

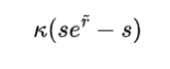
方程（1）

其中s是进入价格，s⋅exp(r̃)是退出价格，r̃是对数回报。现在，保险费的价值是其在风险中性概率测度下的贴现、期望值。假设无风险利率为零，贴现项消失，期望值如下：

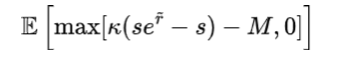
方程（2）

其中M是AMM资本，不包括违约基金资本。为了对这个术语有直观的了解，首先需要注意的是，如果AMM资本M足够大，则很可能回本，并且保险的价值很低（在这种情况下，max函数的第一个术语对于r̃的大多数实现都是负的，因此max函数的值为0）。其次，如果M为0，保险价值对应于期望的交易员利润（因为保险涵盖了所有的利润）。最后，如果M相对较小，交易员的部分利润可以用AMM资本支付，部分利润必须由保险支付。通过这个假设说明，应该让我们对公式（2）有了直观的了解。

对于对数正态回报，可以通过公式（2）进行评估解析，如果抵押品M是报价货币或基础货币（ETH-USD永续合约为例，是ETH或USD）。如果抵押品是第三种货币（以ETH-USD永续合约为例，是BTC），则没有封闭形式，期望值需要通过Monte Carlo方法计算。关于这种近似值的细节，我们参考了白皮书[Maire, Hernandez, 2022]的附录B。

总之，公式（2）为我们提供了AMM希望向交易员收取的保险费，以维持AMM违约基金。

因为定价公式需要在区块链上实施，我们在下一部分中简化了保险费。

银行家的估算方法

银行业估算期望的信用损失为PD * EAD * LGD，详情参见[BIS 2005]，其中PD是违约概率，EAD是违约时的敞口（以货币计算的金额），LGD是违约后的损失（一个相对术语）。也就是说，此方法并非像上述提及的方法那样联合估算期望损失，而是假设违约损失、违约敞口和违约概率之间是独立的。这种方法也用于信用定价，详情参见[Moody’s 2022]。

按照这种思路，我们假设美元损失（EAD * LGD）等于初始头寸值|κ|s。现在，保险费变为

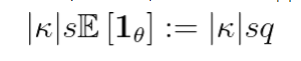
方程（3）

其中1_θ的期望值是违约概率，我们设为q。违约指标在AMM没违约时为0，在违约时为1：

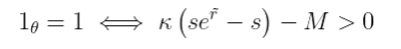
方程（4）

因此，我们的保险费，即公式（2），现在简化为头寸值乘以违约的风险中性概率q。q值对应于数字期权的值。在附录B中，我们提供了为什么这是AMM的保守假设的直观解释。事实上，只要在一个时期内价格至少翻倍的概率很低，它就是保守的。

我们通过数字期权的值乘以交易大小|κ|s来估算保险费。这导致了一个封闭形式的解决方案，我们可以在链上实施。

数字期权的值q可以为所有类型的抵押品M（基础、报价或双币种货币）解析计算，因此我们可以完全在链上实施这种方法。图1比较了保险费近似值和由Eq. (2)给出的期望损失除以κs。

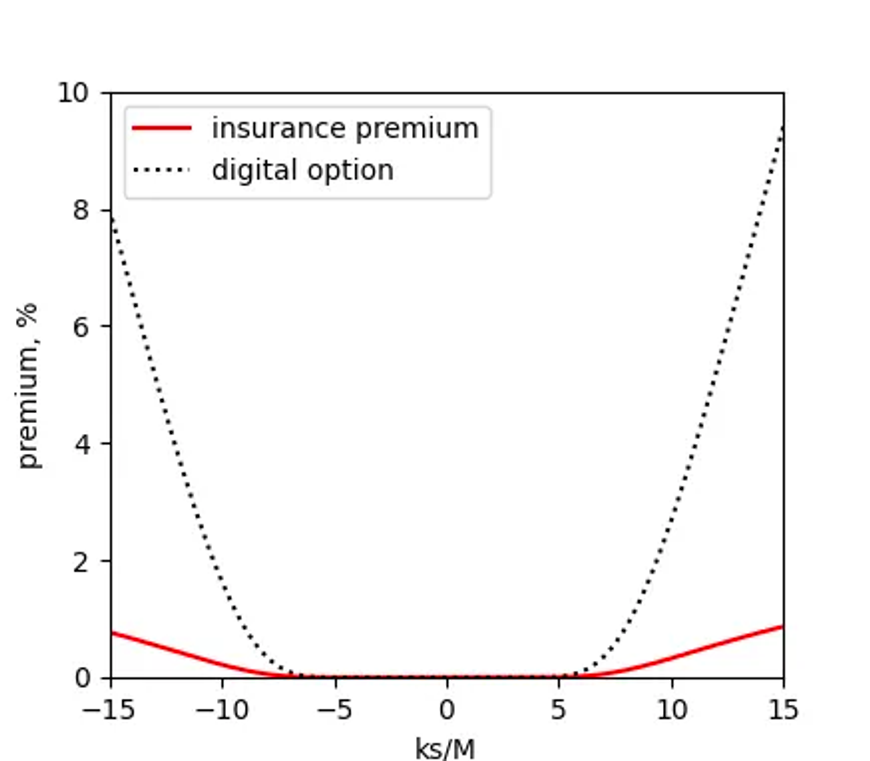
图1：我们用数字期权的值替代了保险费。对于合理的资产波动性，这是一个保守的近似值。在本示例中，我们使用了σ=5%。

随着κs/M的增长，数字期权近似值会高估保险费。 这很有用，因为如果有足够的资本（κs/M比例偏低），我们就会对风险进行充分定价，并且随着资本相对于交易者风险敞口的减少，我们开始对风险定价过高。 因此，定价会抑制交易者让AMM承受过度风险，并激励相反的交易进入，因为回扣同样定价过高（因此有利于交易者），正如我们在下一节中详细介绍的那样。

交易者激励措施

我们将溢价q(κ)计入价格p的方式如下：

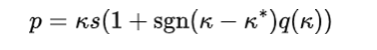
公式（7）

其中，如果sgn(.)的参数为正，则计算结果为1，否则计算结果为-1，κ是最小化AMM风险的交易规模。 这意味着，例如，如果您是空头交易者且κ为负数，您可以在现货价格s上方进行空头交易，这样您就可以在价格向现货收敛时获利； 相反，多头交易者进入现货上方，这与现货交易相比是昂贵的。

正如我们在图1中看到的，对于较低的人均交易规模(κs/M)值，近似值（“数字期权”）保持接近准确的保险价值，并且如果 AMM 面临较高的风险，则会高估保险费。 该溢价向增加风险的交易者收取，并向降低风险的交易者返还。 因此，交易者有动力将AMM净敞口降低至最低点κ-κ*。 在κ-κ*处，AMM的市场风险最小。

结论

我们提出了一个新的永续合约AMM，其基于衍生品定价理论。我们的方法是假设交易员购买信用保险，以确保他们的头寸在合约结束时得到支付。我们的方法是保守的，因为我们估计了违约的风险中性概率，而不是联合估算期望损失。我们的方法可以完全在链上实施，它导致了封闭形式的解决方案。

这是一个技术性的文章，但我们希望能为那些对DeFi和金融工程感兴趣的人提供有趣的观点。我们相信，通过将传统金融的最佳实践与区块链技术相结合，我们可以为DeFi社区提供更好的产品和服务。